题目内容
5. 如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.
如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.(1)求A,B两点的坐标;
(2)若△OC′B′与△OCB关于直线y=x对称,试求C′,B′两点的坐标.
分析 (1)根据等边三角形三线合一的性质求出AC和BC的长,并由勾股定理求高线OC的长,写出A、B两点的坐标;
(2)根据对称的性质得:△BCO≌△B′C′O,且OC′在x轴上,从而求C′,B′两点的坐标.
解答 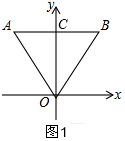 解:(1)如图1,∵△OAB是等边三角形,且AB⊥OC,
解:(1)如图1,∵△OAB是等边三角形,且AB⊥OC,
∴AC=BC=$\frac{1}{2}$AB=6,
∵OB=12,
由勾股定理得:OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=$\sqrt{108}$=6$\sqrt{3}$,
∴A(-6,6$\sqrt{3}$),B(6,6$\sqrt{3}$);
(2)如图2,
∵△OC′B′与△OCB关于直线y=x对称,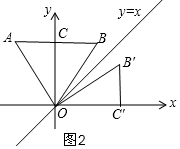
又∵OC在y轴上,
∴OC′在x轴上,OC′=OC=6$\sqrt{3}$,且△BCO≌△B′C′O,
∴∠OC′B′=∠OCB=90°,B′C′=BC=6,
∴B′(6$\sqrt{3}$,6),C′(6$\sqrt{3}$,0).
点评 本题考查了等边三角形的性质、勾股定理、直线y=x的图象及几何变换,明确对称的两个全等是全等形,熟练掌握等边三角形三线合一的性质,在一次函数中,直线y=x属于特殊的直线,该直线与x轴和与y轴的夹角为45°.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.两堆棋子,将第一堆的3个棋子移动到第二堆之后,现在第二堆的棋子数是第一堆棋子的3倍,设第一堆原有m个棋子,则第二堆的棋子原有( )个.
| A. | 3m | B. | 3m-3 | C. | $\frac{m+3}{3}$ | D. | 3m-12 |
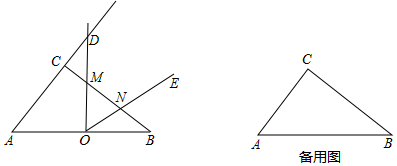


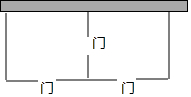 某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?
某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?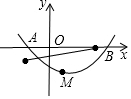 已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.
已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.