题目内容
1.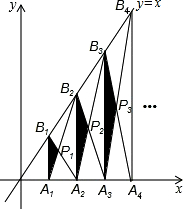 如图,已知A1,A2,…,An,An+1在x轴上,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,…,An,An+1作x轴的垂线交直线y=x于点B1,B2,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次为S1,S2,…,Sn,则S1=$\frac{1}{6}$,Sn=$\frac{{n}^{2}}{4n+2}$.
如图,已知A1,A2,…,An,An+1在x轴上,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,…,An,An+1作x轴的垂线交直线y=x于点B1,B2,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次为S1,S2,…,Sn,则S1=$\frac{1}{6}$,Sn=$\frac{{n}^{2}}{4n+2}$.
分析 根据图象上点的坐标性质得出点B1、B2、B3、…、Bn、Bn+1各点坐标,进而利用相似三角形的判定与性质得出S1、S2、S3、…、Sn,进而得出答案.
解答 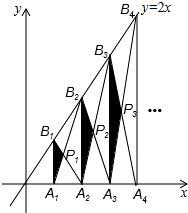 解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,
解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,1),B2(2,2),B3(3,3),…,Bn(n,n)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴$\frac{A{{\;}_{1}B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{1}{2}$,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:$\frac{1}{3}$,
∴S${\;}_{△{A}_{1}{B}_{1}{P}_{1}}$=$\frac{1}{3}$×$1×\frac{1}{2}$=$\frac{1}{6}$,
同理可得:S${\;}_{△{A}_{2}{B}_{2}{P}_{2}}$=$\frac{2}{5}$,S△A3B3P3=$\frac{9}{14}$,
∴Sn=$\frac{{n}^{2}}{4n+2}$.
故答案为$\frac{1}{6}$、$\frac{{n}^{2}}{4n+2}$.
点评 此题主要考查了一次函数函数图象上点的坐标性质得出B点坐标变化规律进而得出S的变化规律,得出图形面积变化规律是解题关键.

练习册系列答案
相关题目
12.四张质地、大小相同的卡片上,分别画上如图所示的四个图形,在看不到图形的情况下从中任意抽出一张卡片,则抽出的卡片上的图形是中心对称图形的概率为( )
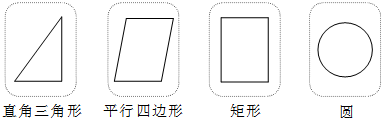

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | 1 |
9.下列二次根式中,能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{20}$ | B. | $\sqrt{12}$ | C. | $\sqrt{8}$ | D. | $\sqrt{4}$ |
6.中国国家图书馆是亚洲最大的图书馆,截止到今年初馆藏图书达3119万册,其中古籍善本约有2000000册.2000000用科学记数法可以表示为( )
| A. | 0.2×107 | B. | 2×106 | C. | 20×105 | D. | 10×26 |
13. 如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
 如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
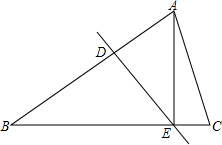 如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E
如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E