题目内容
12．
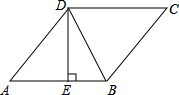如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，则tan∠DBE的值等于2．
分析 直接利用菱形的性质得出AD=AB，再利用锐角三角函数关系表示出AE，AD的长，进而求出DE，BE的长进而得出．
解答 解：∵在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，
∴$\frac{AE}{AD}$=$\frac{3}{5}$，AD=AB，
∴设AE=3x，则AD=5x，
故DE=4x，则BE=5x-3x=2x，
∴tan∠DBE=$\frac{DE}{BE}$=$\frac{4x}{2x}$=2．
故答案为：2．
点评 此题主要考查了菱形的性质以及勾股定理、锐角三角函数关系等知识，正确表示出DE，BE的长是解题关键．
练习册系列答案
相关题目
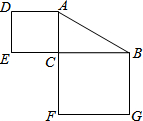如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为225．
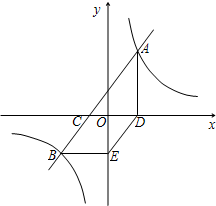如图，已知直线AB与x轴交于点C，与双曲线y=$\frac{k}{x}$交于A（3，$\frac{20}{3}$）、B（-5，a）两点．AD⊥x轴于点D，BE∥x轴且与y轴交于点E．