题目内容
如图，一次函数y1＝x＋b与一次函数y2＝kx＋4的图象交于点P（1，3），则关于x的不等式x＋b＞kx＋4的解集是（ ）
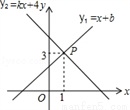
A. x＞﹣2 B. x＞0 C. x＞1 D. x＜1
C 【解析】试题分析：当x＞1时，x+b＞kx+4， 即不等式x+b＞kx+4的解集为x＞1． 故选：C． 考点：一次函数与一元一次不等式．在元旦联欢晚会上，有A、B、C三名同学站在一个三角形的三个顶点上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为游戏公平，则凳子应放的最适当的位置是△ABC的（ ）
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边上高的交点 D. 三边垂直平分线的交点
查看答案下列各组数不能作为直角三角形边长的是（ ）
A. 3，4，5 B. 8，15，17 C. 7，9，11 D. 9，12，15
查看答案如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开．若测得AM的长为1.2km，则M，C两点间的距离为（ ）
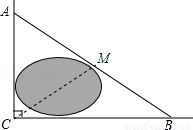
A. 0.5km B. 0.6km C. 0.9km D. 1.2km
查看答案如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（ ）
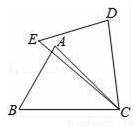
A. BC=EC，∠B=∠E B. BC=EC，AC=DC C. BC=DC，∠A=∠D D. ∠B=∠E，∠A=∠D
查看答案下列各数中，3.141 59，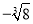 
，0.131 131 113…，－π， 
， 
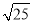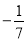，无理数的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案 试题属性- 题型：单选题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一元二次方程x(x－3)＝4的解是( )
A. 1 B. 4 C. －1或4 D. 1或－4
C 【解析】试题解析：∵x（x-3）=4， ∴x2-3x-4=0， ∴（x-4）（x+1）=0， ∴x-4=0或x+1=0， ∴x1=4，x2=-1． 故选C．已知：点P是∠MAN的角平分线上一点，PB⊥AM于B，PC⊥AN于C.
（1）如图1，点D、E分别在线段AB、AC上，且∠DPE=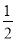
∠BPC，求证：DE=BD+CE；
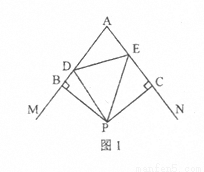
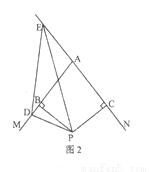
（2）如图2，若D在AB的延长线上，E在直线AC上，则DE、BD、CE三者的数量关系变化吗？若变化，请直接写出结论即可。
阅读下列材料：
（1）解方程：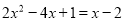 
【解析】
方程化为：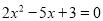 
.
即化为：（2x-3）（x-1）=0，
∴ 2x-3=0或x-1=0，
解得：x=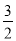
或x=1.
∴方程的根为：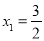 
， 
.
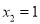（2）求解分式方程的过程是：将分式方程化为整式方程，然后求解整式方程，然后将整工方程的根代入验根，舍去增根，得到的根就是原方程的根.
参考上述材料，解决下列问题：
（1）解方程：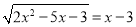 
；
（2）若方程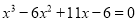
的一个解是x=1，则方程的其他解是__________.
已知：如图，Rt△ABC中，∠BAC=90°.
（1）按要求作图：（保留作图痕迹）
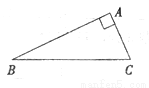
①延长BC到点D，使CD=BC；
②延长CA到点E，使AE=2CA；
③连接AD，BE并猜想线段AD与BE的大小关系；
（2）证明（1）中你对线段AD与BE大小关系的猜想.
【解析】
（1）AD与BE的大小关系是________________.
（2）证明：
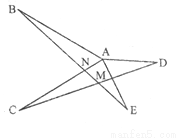
查看答案已知：如图，AB=AC，AD=AE，∠BAC=∠DAE=α，BE与AC、CD分别相交于点N、M.
（1）求证：BE=CD；
（2）求∠BMC的大小.（用α表示）
2017年9月17日，金秋的北京，我校初二全体同学到距学校30千米的房山农业职业学院，参加为期一周的学农劳动。同学们乘坐大巴车前往，李老师因学校有事晚出发了5分钟，开私家车前往，结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍，求大巴车和李老师开的私家车的速度分别是多少？
查看答案 试题属性- 题型：单选题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
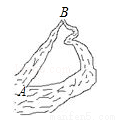
如图，把弯曲的河道改直，能够缩短航程，这样做根据的道理是_____．
如图所示，边长为a的正方形中阴影部分的面积为（ ）
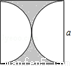
A. a2﹣π（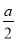
）2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
下列各组整式中不是同类项的是（ ）
A. 3a2b与﹣2ba2 B. 2xy与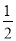
yx C. 16与﹣
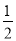D. ﹣2xy2与3yx2
单项式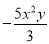
的系数与次数分别是（ ）
A.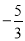 
和3 B. ﹣5和3 C. 
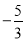和2 D. ﹣5和2
对于圆的周长公式C=2πR，下列说法错误的是（ ）
A. π是变量 B. R、C是变量 C. R是自变量 D. C是因变量
查看答案下列式子中，符合代数式的书写格式的是（ ）
A．（a﹣b）×7 B．3a÷5b C．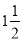
ab D．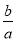
- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
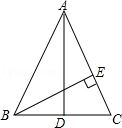
如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．
求下列各式中的x．
(1)4x2 ＝81；
(2)(x＋1)3－27＝0．
(3)计算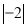
＋(3－π)0－2－1＋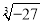
如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为 ．
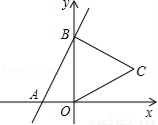
将一次函数y=-x+3的图像沿y轴向下平移2个单位长度，所得图像对应的函数表达式为__________．
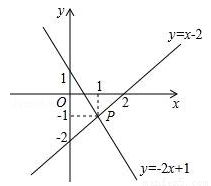
查看答案如图，已知函数y=x-2和y=-2x+1的图象交于点P，根据图象可得方程组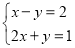
的解是 ．
已知a、b、c是△ABC的三边长，且满足关系式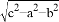
+|a﹣b|=0，则△ABC的形状为_____．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
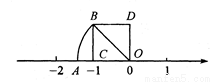
如图，在正方形ODBC中，若OC=1，OA=OB，则数轴上点A表示的数是__________．
某人一天饮水1890mL，用四舍五入法对1890mL精确到1000mL表示为____mL．
查看答案在平面直角坐标系中，点（2，-3）在第____象限．
查看答案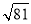
的平方根为_____．
关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A. 点(0,k)在l上
B. l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大
D. l经过第一、二、三象限
查看答案如图，一次函数y1＝x＋b与一次函数y2＝kx＋4的图象交于点P（1，3），则关于x的不等式x＋b＞kx＋4的解集是（ ）
A. x＞﹣2 B. x＞0 C. x＞1 D. x＜1
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各数中，3.141 59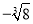， ，0.131 131 113…，－π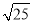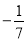， ， ，无理数的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】无限不循环小数为无理数，由此可得出无理数的个数． 【解析】 由定义可知无理数有：0.131131113…，?π，共两个. 故选：B.在下列“禁毒”“和平”“志愿者”“节水”这四个标志中，属于轴对称图形的是( )
A. 
B. 
C. 
D. 
从2012年4月1日起厦门市实行新的自来水收费阶梯水价，收费标准如下表所示：
月用水量 | 不超过15吨的部分 | 超过15吨不超过25吨的部分 | 超过25吨的部分 |
收费标准 （元/吨） | 2.2 | 3.3 | 4.4 |
备注：①．每月居民用水缴费包括实际用水的水费和污水处理费两部分．
②．以上表中的价格均不包括1元/吨的污水处理费
（1）某用户12月份用水量为20吨，则该用户12月份应缴水费是多少？
（2）若某用户的月用水量为m吨，请用含m的式子表示该用户月所缴水费．
查看答案小明乘公共汽车到东方明珠玩，小明上车时，发现车上已有（6a﹣2b）人，车到中途时，有一半人下车，但又上来若干人，这时公共汽车上共有（10a﹣6b）人，则中途上车多少人？当a=5，b=3时，中途上车的人数．
查看答案定义：若a+b=2，则称a与b是关于1的平衡数．
（1）3与 是关于1的平衡数，5﹣x与 是关于1的平衡数．（用含x的代数式表示）
（2）若a=2x2﹣3（x2+x）+4，b=2x﹣[3x﹣（4x+x2）﹣2]，判断a与b是否是关于1 的平衡数，并说明理由．
查看答案某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
（1）生产量最多的一天比生产量最少的一天多生产多少辆?
（2）本周总的生产量是多少辆?
查看答案 试题属性- 题型：单选题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在数轴上表示下列各数，并用“＜”连接起来．
﹣4，﹣|﹣2.5|，﹣（﹣2），0，﹣12．
﹣4＜﹣|﹣2.5|＜﹣12＜0＜﹣（﹣2） 【解析】试题分析：首先在数轴上确定表示各数的点的位置，然后再根据在数轴上表示的有理数，右边的数总比左边的数大用“＜“号排列即可． 试题解析：如图： ， ﹣4＜﹣|﹣2.5|＜﹣12＜0＜﹣（﹣2）． 【点睛】本题考查了在数轴上表示数，利用数轴比较有理数的大小，正确描点，熟练掌握数轴上的数右边的总比左边的大是解题的关键. ...先化简，再求值：x2﹣3（2x2﹣4y）+2（x2﹣y）其中x=﹣2，y=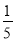
．
化简：
（1）﹣3xy﹣2y2+5xy﹣4y2
（2）2（5a2﹣2a）﹣4（﹣3a+2a2）
查看答案计算：
（1）3+（﹣11）﹣（﹣9）
（2）（﹣7）×5﹣（﹣36）÷4
（3）（1﹣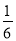
+
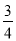）×（﹣24）
（4）﹣14+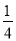
×[2×（﹣6）﹣（﹣4）2]．
让我们轻松一下，做一个数字游戏：
第一步：取一个自然数n1=5，计算n12+1得a1；
第二步：算出a1的各位数字之和得n2，计算n22+1得a2；
第三步：算出a2的各位数字之和得n3，再计算n32+1得a3；
…
依此类推，则a2013=_____．
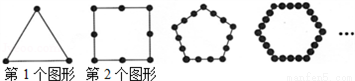
查看答案如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是___________．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一个多项式加上多项式2x﹣1后得3x﹣2，则这个多项式为（ ）
A. x﹣1 B. x+1 C. x﹣3 D. x+3
A 【解析】根据题意得：（3x﹣2）﹣（2x﹣1）=3x﹣2﹣2x+1=x﹣1， 故选A. 【点睛】本题考查了整式的加减，去括号的法则，合并同类项的运用，在去括号时注意符号的变化．下列式子中，不能成立的是（ ）
A. ﹣（﹣2）=2 B. ﹣|﹣2|=﹣2 C. 23=6 D. （﹣2）2=4
查看答案若有理数a的值在﹣1与0之间，则a的值可以是（ ）
A. ﹣2 B. 1 C.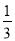 
D.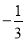 
下列运算正确的是（ ）
A. 3a+2b=5ab B. 3a2b﹣3ba2=0 C. 3x2+2x3=5x5 D. 5y2﹣4y2=1
查看答案下列各组是同类项的是（ ）
A. a3与a2 B.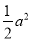 
与2a2 C. 2xy与2y D. 3与a
﹣3的相反数是（ ）
A. 3 B. ﹣3 C. -
D.
- 题型：单选题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某商家预测一种衬衫能畅销市场，就用12000元购进了一批这种衬衫，上市后果然供不应求，商家又用了26400元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但每件进价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫都按每件150元的价格销售，则两批衬衫全部售完后的利润是多少元？
(1) 该商家购进的第一批衬衫是120件．(2) 两批衬衫全部售完后的利润是15600元． 【解析】试题分析：（1）设第一批衬衫x件，则第二批衬衫为2x件，接下来依据第二批衬衫每件进价贵了10元列方程求解即可； （2）先求得每一批衬衫的数量和进价，然后再求得两批衬衫的每一件衬衫的利润，最后根据利润=每件的利润×件数求解即可． 试题解析：（1）设第一批衬衫x件，则第二批衬衫为2x件．根...若x=2m+1，y=3+4m．
（1）请用含x的代数式表示y；
（2）如果x=4，求此时y的值．
查看答案解答一个问题后，将结论作为条件之一，提出与原问题有关的新问题，我们把它称为原问题的一个“逆向”问题．例如，原问题是“若矩形的两边长分别为3和4，求矩形的周长”，求出周长等于14后，它的一个“逆向”问题可以是“若矩形的周长为14，且一边长为3，求另一边的长”；也可以是“若矩形的周长为14，求矩形面积的最大值”，等等．
（1）设A=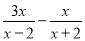
，B=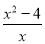
，求A与B的积；
（2）提出（1）的一个“逆向”问题，并解答这个问题．
查看答案按要求完成下列各题：
（1）已知实数a、b满足（a+b）2=1，（a﹣b）2=9，求a2+b2﹣ab的值；
（2）已知（2015﹣a）（2016﹣a）=2047，试求（a﹣2015）2+（2016﹣a）2的值．
查看答案请先将下式化简，再选择一个适当的数代入求值．（1﹣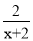
）﹣
÷
．
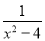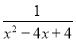解方程
（1）
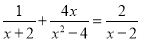（2）
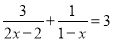
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧