题目内容
12.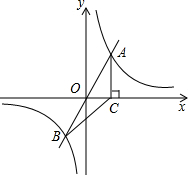 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{6}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,则△ABC的面积等于6.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{6}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,则△ABC的面积等于6.
分析 由正、反比例函数图象的对称性可得点A、B关于原点O对称,进而可得出S△BOC=S△AOC,由S△ABC=S△AOC+S△BOC结合反比例函数系数k的几何意义,即可求出△ABC的面积.
解答 解:由正、反比例函数图象的对称性可知:点A、B关于原点O对称,
∴S△BOC=S△AOC=$\frac{1}{2}$k=3,
∴S△ABC=S△AOC+S△BOC=3+3=6.
故答案为:6.
点评 本题考查了反比例函数与一次函数的交点问题、正(反)比例函数的图象以及反比例函数系数k的几何意义,由正、反比例函数图象的对称轴找出S△BOC=S△AOC是解题的关键.

练习册系列答案
相关题目
3.-|-125|的立方根是( )
| A. | -$\frac{25}{3}$ | B. | $\frac{25}{3}$ | C. | 5 | D. | -5 |
20. 如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
 如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
17.下列运算不正确的是( )
| A. | a2•a3=a5 | B. | (-a)4=a4 | C. | a2+a3=a5 | D. | (a2)3=a6 |
4.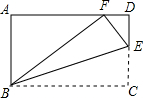 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{5}{3}$ |
1.在平面直角坐标系中,点P(-2,$\sqrt{3}$)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.将不等式x-1>0的解集表示在数轴上,下列表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示: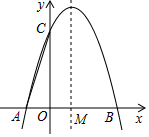 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.