题目内容
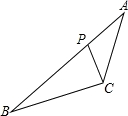
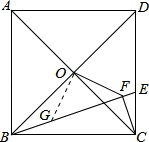
如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为__________.

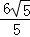 .
.
【考点】全等三角形的判定与性质;等腰直角三角形;正方形的性质.
【专题】计算题;几何图形问题.
【分析】在BE上截取BG=CF,连接OG,证明△OBG≌△OCF,则OG=OF,∠BOG=∠COF,得出等腰直角三角形GOF,在RT△BCE中,根据射影定理求得GF的长,即可求得OF的长.
【解答】解:如图,在BE上截取BG=CF,连接OG,
∵RT△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中

∴△OBG≌△OCF(SAS)
∴OG=OF,∠BOG=∠COF,
∴OG⊥OF,
在RT△BCE中,BC=DC=6,DE=2EC,
∴EC=2,
∴BE=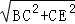 =
=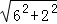 =2
=2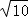 ,
,
∵BC2=BF•BE,
则62=BF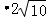 ,解得:BF=
,解得:BF=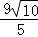 ,
,
∴EF=BE﹣BF= ,
,
∵CF2=BF•EF,
∴CF=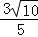 ,
,
∴GF=BF﹣BG=BF﹣CF=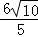 ,
,
在等腰直角△OGF中
OF2= GF2,
GF2,
∴OF=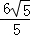 .
.
故答案为: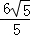 .
.
【点评】本题考查了全等三角形的判定和性质,直角三角形的判定以及射影定理、勾股定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,点C的坐标为
,点C的坐标为 ,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )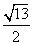 ;B.
;B. ; C.
; C. ;D.
;D. ;
;