题目内容
【题目】某校开展拓展课程展示活动,需要制作A,B两种型号的宣传广告共20个,已知A,B两种广告牌的单价分别为40元,70元
(1)若根据活动需要,A种广告牌数量与B种广告牌数量之比为3:2,需要多少费用?
(2)若需制作A,B两种型号的宣传广告牌,其中B种型号不少于5个,制作总费用不超过1000元,则有几种制作方案?每一种制作方案的费用分别是多少?
【答案】(1) 1040元;(2)方案有2种: A 14个,B 6个,980元; A 15个,B种5个,1100元.
【解析】
(1)巧设未知数,用3x与2x的和等于20构建方程求出A、B两种广告牌数量,然后代入即可得出答案;
(2)题构建不等式组求出A、B两种广告牌数量的取值范围,由总价=单价×数量求出两种方案的费用.
解:(1)设A、B两种广告牌数量分别为3x个和2x个,依题意得;
3x+2x=20,
解得:x=4,
A种广告牌数量为12个,B种广告牌数量为8个;
这次活动需要的费用为:12×40+70×8=1040(元).
答:A种广告牌数量与B种广告牌数量之比为3:2,需要费用1040元.
(2)设A种广告牌数量为x个,则B种广告牌数量为(20-y)个,依题意得:
![]()
解得![]() ,
,
又∵y取正整数,
∴y=14或15,
又∵B种种广告牌数量不少于5个.
∴制作A,B两种型号的宣传广告牌有两种方案:
①A种广告牌数量为14个,B种广告牌数量为6个;
②A种广告牌数量为15个,B种广告牌数量为5个.
其费用如下:
①14×40+70×6=980(元)
②15×50+70×5=1100(元)
答:有2种方案;其费用分别为980元和1100元.

 小学夺冠AB卷系列答案
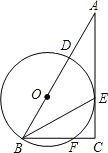
小学夺冠AB卷系列答案【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
【题目】当今,青少年用电脑手机过多,视力水平下降已引起了全社会的关注,某校为了解八年级1000名学生的视力情况,从中抽查了150名学生的视力情况,通过数据处理,得到如下的频数分布表.解答下列问题:
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?