��Ŀ����
����Ŀ����ͼ����֪������![]() ��
��![]() ��������
��������![]() ����
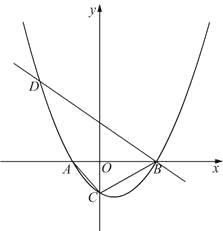
����![]() ������������ν���A,B���㣬��
������������ν���A,B���㣬��![]() �ύ�ڵ�C��������B��ֱ��
�ύ�ڵ�C��������B��ֱ��![]() �������ߵ���һ����ΪD.
�������ߵ���һ����ΪD.
��1������D�ĺ�����Ϊ-5���������ߵĺ�������ʽ��
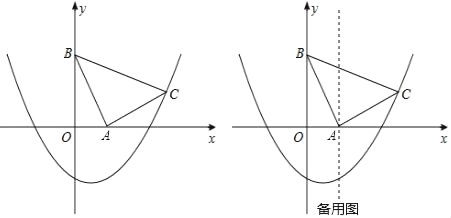
��2�����ڵ�һ�������������е�P��ʹ����A��B��PΪ���������������ABC���ƣ���![]() ��ֵ��
��ֵ��
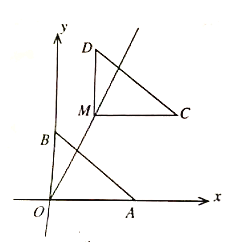
��3���ڣ�1���������£���FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ. ����F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��F
����3��F![]() .
.
��������
���⣨1�����ݵ��������ϵ���������㷽�̵Ĺ�ϵ���������![]() ��ֵ�õ�ֱ�ߵĽ���ʽ����D�������ꡢ
��ֵ�õ�ֱ�ߵĽ���ʽ����D�������ꡢ![]() ��ֵ�õ������ߵĺ�������ʽ.
��ֵ�õ������ߵĺ�������ʽ.
��BM=9��AB=6����BF=![]() ��BD=
��BD=![]() ��AF=
��AF=![]()
��2������PAB�ס�ABC����PAB�ס�BAC����������ۼ���.
��3������D��DH��y���ڵ�H������A��AG��DH�ڵ�G����BD�ڵ�F�����F��Ϊ���������ǣ����ڵ�M���߶�AF����ÿ��1����λ���ٶ��˶������߶�FD����ÿ��2����λ���ٶ��˶����Ӷ�����ֱ��BD����б����30��֪��![]() ���ָ��ݴ�ֱ�߶���̵�����֪��F��Ϊ���Ӷ����ݺ�30��ֱ�������ε�������⼴��.
���ָ��ݴ�ֱ�߶���̵�����֪��F��Ϊ���Ӷ����ݺ�30��ֱ�������ε�������⼴��.
�����������1����������![]() ��
��![]() ��������
��������![]() ����
����![]() ������������ν���A,B���㣬
������������ν���A,B���㣬
��A��-2��0����B��4��0��.
����B��ֱ��![]() �ϣ���
�ϣ���![]() ����
����![]() .
.
��ֱ�ߵĽ���ʽΪ![]() .
.
����D��ֱ��![]() �ϣ��Һ�����Ϊ-5����������Ϊ
�ϣ��Һ�����Ϊ-5����������Ϊ![]() .
.
����D��������![]() �ϣ���
�ϣ���![]() �����
�����![]() .
.
�������ߵĺ�������ʽΪ![]() .
.
��2���ã���C������Ϊ![]() ����
����![]() .
.
���P������Ϊ![]() ��
��
�����������
������PAB�ס�ABC������PAB=��ABC��![]() .
.
������PAB=��ABC ��![]() ����
����![]() .
.
��![]() �����
�����![]() .
.
��ʱ��P������Ϊ![]() ��
��![]() ��
��
����![]() ��
��![]() �����
�����![]() .
.
������PAB�ס�BAC������PAB=��BAC��![]() .
.
������PAB=��BAC ��![]() ����
����![]() .
.
��![]() �����
�����![]() .
.
��ʱ��P������Ϊ![]() ��
��![]() ��
��
����![]() ��
��![]() �����
�����![]() .
.

��3����ͼ������D��DH��y���ڵ�H������A��AG��DH�ڵ�G����BD�ڵ�F�����F��Ϊ����.
��ֱ��BD�Ľ���ʽΪ![]() �����FBA=��FGD=30��.
�����FBA=��FGD=30��.
��AB=6����AF=![]() .
.
����F������Ϊ![]() .
.