题目内容
19.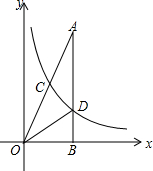 如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.
如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.(1)求点D的坐标(用含m的式子表示);
(2)连接OD,若OD平分∠AOB,求反比例函数的解析式.
分析 (1)过点C作CE⊥OB于点E,根据∠ABO=90°得到CE∥AB,因为点C(1,m)为OA的中点,所以点E为OB的中点,所以OB=2OE=2,得到点D的横坐标为2,设反比例函数的解析式为y=$\frac{k}{x}$,把点C(1,m)代入得:k=m,得到y=$\frac{m}{x}$,x=2时,y=$\frac{m}{2}$,所以点D的坐标为(2,$\frac{m}{2}$).
(2)过点D作DF⊥AO于点F,先求出点D的坐标为(2,$\frac{m}{2}$),根据角平分线的性质得到DF=DB=$\frac{m}{2}$,根据点C(1,m)求出OC,得到OA=2OC=$\sqrt{{1}^{2}+{m}^{2}}$,根据S△ABO=S△OBD+S△AOD,即可解答.
解答 解:(1)如图1,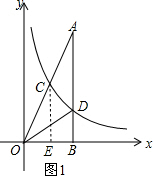 ,
,
过点C作CE⊥OB于点E,
∵∠ABO=90°
∴CE∥AB,
∵点C(1,m)为OA的中点,
∴点E为OB的中点,
∴OB=2OE=2,
∴点D的横坐标为2,
设反比例函数的解析式为y=$\frac{k}{x}$,
把点C(1,m)代入得:k=m,
∴y=$\frac{m}{x}$,
当x=2时,y=$\frac{m}{2}$,
∴点D的坐标为(2,$\frac{m}{2}$).
(2)如图2,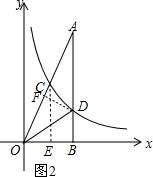
过点D作DF⊥AO于点F,
∵OD平分∠AOB,
∴DF=BD,
∵点D的坐标为(2,$\frac{m}{2}$),
∴DF=DB=$\frac{m}{2}$,
∵点C(1,m)
∴OC=$\sqrt{{1}^{2}+{m}^{2}}$,
∴OA=2OC=2$\sqrt{{1}^{2}+{m}^{2}}$,
∵S△ABO=S△OBD+S△AOD,
即$\frac{1}{2}OB•AB=\frac{1}{2}OB•BD+\frac{1}{2}AO•DF$
$\frac{1}{2}×2•2m=\frac{1}{2}×2•\frac{m}{2}+\frac{1}{2}×2\sqrt{1+{m}^{2}}•\frac{m}{2}$
解得:m=2$\sqrt{2}$,
∴反比例函数的解析式为:y=$\frac{2\sqrt{2}}{x}$.
点评 本题考查反比例函数,解决本题的关键是明确反比例函数图象上点的坐标特征.

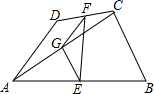 如图,四边形ABCD中,AD=BC,E、F、G分别是AB、DC、AC的中点.若∠ACB=
如图,四边形ABCD中,AD=BC,E、F、G分别是AB、DC、AC的中点.若∠ACB=64°,∠DAC=22°,则∠EFG的度数为( )
| A. | 42° | B. | 38° | C. | 32° | D. | 21° |
| A. | a2m-n-2 | B. | a2-n | C. | a2m+n-2 | D. | an-2 |
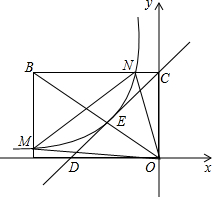 如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.
如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1. 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n). 如图,已知点A(1,1),B(4,1),则线段AB上任意一点的坐标可表示为y=1(1≤x≤4).
如图,已知点A(1,1),B(4,1),则线段AB上任意一点的坐标可表示为y=1(1≤x≤4).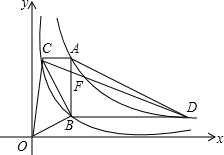 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0). 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)