Question

1．已知AB、AC是⊙O的弦，半径是1，AB=$\sqrt{2}$，AC=$\sqrt{3}$，则∠BAC=15°或75°．

Answer 1

分析 根据垂径定理和特殊角的三角函数值，分两种情况计算即可．

解答 解：分别作OD⊥AB，OE⊥AC，垂足分别是D、E．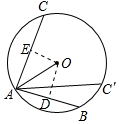
∵OE⊥AC，OD⊥AB，根据垂径定理得AE=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$，AD=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$，
∴sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{3}}{2}$，sin∠AOD=$\frac{AD}{AO}$=$\frac{\sqrt{2}}{2}$，
根据特殊角的三角函数值可得∠AOE=60°，∠AOD=45°，
∴∠BAO=45°，∠CAO=90°-60°=30°，
∴∠BAC=45°+30°=75°，
或∠BAC′=45°-30°=15°．
15°或75°．

点评 此题主要考查了垂径定理和勾股定理，灵活运用相关定理是解题的关键，注意要考虑到两种情况．