Question

如图，点A是半圆上的一个三等分点，点B是弧AN的中点，点P是直径MN上一个动点，圆O的半径为1，
（1）找出当AP+BP能得到最小值时，点P的位置，并证明
（2）求出AP+BP最小值．

Answer 1

分析：（1）本题是要在MN上找一点P，使PA+PB的值最小，根据“两点之间线段最短”，设A′是A关于MN的对称点，连接A′B，与MN的交点即为点P；
（2）可证△OA′B是等腰直角三角形，从而得出结果．

解答：（1）证明：过A作AA′⊥MN于E，连接BA′．

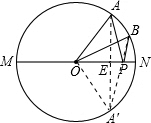
∵MN过圆心O，
∴AE=EA′，
∴AP=PA′，即AP+BP=PA′+BP，
根据两点间线段最短，当A′，P，B三点共线时，PA′+BP=BA'，
AP+BP此时为最小值，
∴P位于A′B与MN的交点处；
（2）解：∵点A是半圆上的一个三等分点，
∴∠AON=∠A'ON=60°，
∵点B是弧AN的中点，
∴

AB

=

BN

，
∴∠BON=30°，
∴∠BOA'=∠A'ON+∠BON=90°，
∵OB=OA=1，
∴BA′=

2

，即AP+BP最小值为

2

．

点评：本题考查轴对称-最短路径问题，正确确定P点的位置是解题的关键，确定点P的位置这类题在课本中有原题，因此加强课本题目的训练至关重要．