题目内容
如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C和D两点，AB=10cm，CD=6cm，则AC长为
- A.0.5cm
- B.1cm
- C.1.5cm
- D.2cm
D
分析：作出弦心距OE，垂足为E，根据垂径定理可以求出AE、CE的长，再求AC也就不难了．
解答：
解：作OE⊥AB，垂足为E，由垂径定理知，点E是CD的中点，也是AB的中点
∴AE=
AB=5，CE=CD=3
∴AC=AE-CE=5-3=2cm
故选D．
点评：本题利用了垂径定理：垂直于弦的直径平分弦求解．
分析：作出弦心距OE，垂足为E，根据垂径定理可以求出AE、CE的长，再求AC也就不难了．
解答：
解：作OE⊥AB，垂足为E，由垂径定理知，点E是CD的中点，也是AB的中点∴AE=
AB=5，CE=CD=3∴AC=AE-CE=5-3=2cm
故选D．
点评：本题利用了垂径定理：垂直于弦的直径平分弦求解．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
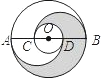如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为
9、如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为（ ）
（2006•静安区二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E
如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B．若OM=2，OP=1，MA=AB=BC，则△MBQ的面积为
如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为（ ）