题目内容
15. 如图,在△ABC中,D为BC上的一点,AC=4,CD=3,AD=5,AB=4$\sqrt{5}$.
如图,在△ABC中,D为BC上的一点,AC=4,CD=3,AD=5,AB=4$\sqrt{5}$.(1)求证:∠C=90°;
(2)求BD的长.
分析 (1)根据勾股定理的逆定理可证∠C=90°;
(2)在Rt△ACB中,先根据勾股定理得到BC的长,再根据线段的和差关系可求BD的长.
解答 (1)证明:∵AC2+CD2=42+32=25,AD2=52=25,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,且∠C=90°;
(2)解:在Rt△ACB中,∠C=90°
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8,
∴BD=BC-CD=8-3=5.
点评 本题考查了勾股定理的逆定理,勾股定理,注意熟练掌握勾股定理的逆定理和勾股定理是解题的关键.

练习册系列答案
相关题目
10.在△ABC中,AB=5,BC=8,则AC边的长不可能是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
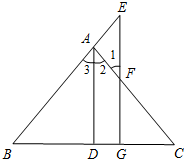 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:∠3=∠2.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:∠3=∠2. 如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.
如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.