Question

【题目】已知,平分，点、、分别是射线、、上的动点（、、不与点重合），连接交射线于点，设.

（1）如图1，若，则：

①的度数为

②当时， ，当时，

（2）如图2，若，则是否存在这样的的值，使得中有两个想等的角？若存在，求出的值；若不存在，说明理由.

Answer 1

【答案】（1）①24°，②108，54；（2）存在，x=42、24、33、123.

【解析】

（1）①运用平行线的性质以及角平分线的定义，可得①∠ABO的度数；②根据∠ABO、∠BAD的度数以及△AOB的内角和，可得x的值；

（2）分两种情况进行讨论：AC在AB左侧，AC在AB右侧，分别根据三角形内角和定理以及直角的度数，可得x的值．

（1）如图1，

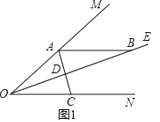
①∵∠MON＝48°，OE平分∠MON，

∴∠AOB＝∠BON＝24°，

∵AB∥ON，

∴∠ABO＝24°；

②当∠BAD＝∠ABD时，∠BAD＝24°，

∵∠AOB＋∠ABO＋∠OAB＝180°，

∴∠OAC＝180°24°×3＝108°；

当∠BAD＝∠BDA时，∵∠ABO＝24°，

∴∠BAD＝78°，∠AOB＝24°，

∵∠AOB＋∠ABO＋∠OAB＝180°，

∴∠OAC＝180°24°24°78°＝54°，

故答案为：①24°；②108，54；

（2）如图2，存在这样的x的值，使得△ADB中有两个相等的角．

∵AB⊥OM，∠MON＝48°，OE平分∠MON，

∴∠AOB＝24°，∠ABO＝66°，

①当AC在AB左侧时：

若∠BAD＝∠ABD＝66°，则∠OAC＝90°66°＝24°；

若∠BAD＝∠BDA＝（180°66°）＝57°，则∠OAC＝90°57°＝33°；

若∠ADB＝∠ABD＝66°，则∠BAD＝48°，故∠OAC＝90°48°＝42°；

②当AC在AB右侧时：

∵∠ABE＝114°，且三角形的内角和为180°，

∴只有∠BAD＝∠BDA＝（180°114°）＝33°，则∠OAC＝90°＋33°＝123°．

综上所述，当x＝24、33、42、123时，△ADB中有两个相等的角．