Question

如图，⊙C经过原点且与两坐标轴分别交于点A（0，2）和点B，D为⊙C在第一象限内的一点，且∠ODB=60°，求⊙C的半径、线段AB的长、B点坐标及圆心C的坐标．

Answer 1

分析：连接AB；由圆周角定理可知，AB必为⊙C的直径；Rt△ABO中，易知OA的长，而∠OAB=∠ODB=60°，通过解直角三角形，即可求得斜边AB的长，也就求得了⊙C的半径；在Rt△ABO中，由勾股定理即可求得OB的长，进而可得到B点的坐标；过C分别作弦OA、OB的垂线，设垂足为E、F；根据垂径定理即可求出OE、OF的长，也就得到了圆心C的坐标．

解答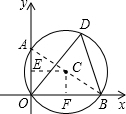：解：如图，连接AB．
∵∠ODB=∠OAB，∠ODB=60°，
∴∠OAB=60°，
∵∠AOB是直角，
∴AB是⊙C的直径，∠OBA=30°；
∴AB=2OA=4；
∴⊙C的半径为2；
在Rt△OAB中，由勾股定理得：OB²+OA²=AB²，
∴OB=2

3

，
∴B的坐标为：（2

3

，0）；
过C点作CE⊥OA于E，CF⊥OB于F，
由垂径定理得：OE=AE=1，OF=BF=

3

，
∴CE=

3

，CF=1，
∴C的坐标为（

3

，1）．
故⊙C的半径为2，线段AB的长，为4，B点坐标为（2

3

，0），圆心C的坐标为（

3

，1）．

点评：此题主要考查了圆周角定理、垂径定理、点的坐标意义、勾股定理等知识的综合应用能力，综合性较强，难度适中．