题目内容
如图,在直角坐标系中,直线y=
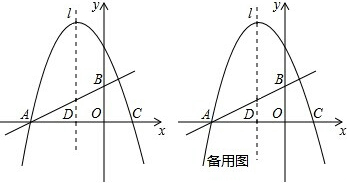
x+1与x轴、y轴的交点分别为A、B,以x=-1为对称轴的抛物线y=-x2+bx+c与x轴分别交于点A、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t.设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;
(3)点M是对称轴上任意一点,在抛物线上是否存在点N,使以点A、B、M、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,说明理由.
| 1 |
| 3 |
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t.设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;
(3)点M是对称轴上任意一点,在抛物线上是否存在点N,使以点A、B、M、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,说明理由.

考点:二次函数综合题
专题:
分析:(1)根据直线方程易求点A的坐标,由抛物线的对称性可以求得点C的坐标;然后写出抛物线的交点式方程即可;
(2)需要分类讨论:①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(-1,4);
②当∠AED=90°时,△AED∽△AOB.过点P作PG⊥AC于点G,则△AED∽△CGD.根据相似三角形的对应边成比例列出关于t的一元二次方程:-t2+2t+3=3(-1-t),通过解该方程可以求得t的值;
(3)需要分类讨论:以AB为边和以AB为对角线时的平行四边形.
(2)需要分类讨论:①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(-1,4);
②当∠AED=90°时,△AED∽△AOB.过点P作PG⊥AC于点G,则△AED∽△CGD.根据相似三角形的对应边成比例列出关于t的一元二次方程:-t2+2t+3=3(-1-t),通过解该方程可以求得t的值;
(3)需要分类讨论:以AB为边和以AB为对角线时的平行四边形.
解答:解:(1)∵直线y=
x+1与x轴交点为A,
∴点A的坐标为(-3,0),
∵抛物线的对称轴为x=-1,
∴点C的坐标为(1,0),
∵抛物线y=-x2+bx+c与x轴分别交于点A、C,
∴抛物线为y=-(x+3)(x-1)=-x2-2x+3;
(2)∵抛物线y=-x2-2x+3的对称轴为x=-1,
∴点D的坐标为(-1,0),
①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(-1,4);
②当∠AED=90°时,△AED∽△AOB.
过点P作PG⊥AC于点G,则△AED∽△PGD.
于是
=
=
=
,
∴PG=3GD.
即:-t2+2t+3=3(-1-t),
解得 t1=-2,t2=3(不合题意,舍去).
当t=2时,-22+2×2+3=3,
所以此时点P的坐标为(-2,3).
综上所述,点P的坐标是(-1,4)或(-2,3);
(3)点N的坐标为:以线段AB为边时,N1(2,-5),N2(-4,-5),
以线段AB为对角线时,N3(-2,3).
综上所述,点N的坐标分别是:N1(2,-5),N2(-4,-5),N3(-2,3).
| 1 |
| 3 |
∴点A的坐标为(-3,0),
∵抛物线的对称轴为x=-1,
∴点C的坐标为(1,0),
∵抛物线y=-x2+bx+c与x轴分别交于点A、C,
∴抛物线为y=-(x+3)(x-1)=-x2-2x+3;
(2)∵抛物线y=-x2-2x+3的对称轴为x=-1,
∴点D的坐标为(-1,0),
①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(-1,4);
②当∠AED=90°时,△AED∽△AOB.
过点P作PG⊥AC于点G,则△AED∽△PGD.
于是
| GD |
| PG |
| DE |
| AE |
| OB |
| OA |
| 1 |
| 3 |

∴PG=3GD.
即:-t2+2t+3=3(-1-t),
解得 t1=-2,t2=3(不合题意,舍去).
当t=2时,-22+2×2+3=3,
所以此时点P的坐标为(-2,3).
综上所述,点P的坐标是(-1,4)或(-2,3);
(3)点N的坐标为:以线段AB为边时,N1(2,-5),N2(-4,-5),
以线段AB为对角线时,N3(-2,3).
综上所述,点N的坐标分别是:N1(2,-5),N2(-4,-5),N3(-2,3).
点评:本题是二次函数的综合题型,其中涉及到的知识点待定系数法求二次函数解析式、相似三角形的判定与性质以及平行四边形的性质.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
若式子
在实数范围内有意义,则x的取值范围是( )
| x-4 |
| A、x≤-4 | B、x≥-4 |
| C、x≤4 | D、x≥4 |
 如图,已知反比例函数y=
如图,已知反比例函数y= 为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60
为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60