题目内容
在一副三角板ABC和DEF中,∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°.

(1)当AB∥DC时,如图①,求∠DCB的度数.
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由.
(3)如图③,当∠DCB等于多少度时,AB∥EC?

(1)当AB∥DC时,如图①,求∠DCB的度数.
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由.
(3)如图③,当∠DCB等于多少度时,AB∥EC?
考点:平行线的判定与性质
专题:
分析:(1)求出∠B,根据平行线的判定推出即可;
(2)求出∠ACE+∠E=180°,根据平行线的判定推出即可;
(3)求出∠BCE=∠B,根据平行线的判定推出即可.
(2)求出∠ACE+∠E=180°,根据平行线的判定推出即可;
(3)求出∠BCE=∠B,根据平行线的判定推出即可.
解答:解:(1)∵∠BCA=90°,∠A=60°,
∴∠B=180°-90°-60°=30°,
∵AB∥CD,
∴∠DCB=∠B=30°;
(2)DE∥AC,
理由是:∵∠EDC=90°,∠DEC=45°,
∴∠DCE=45°,
∵∠BCA=90°,
∴∠ACE+∠DEC=90°+45°+45°=180°,
∴DE∥AC;
(3)当∠DCB等于15度时,AB∥EC,
理由是:∵∠DCB=15°,∠DCE=45°,
∴∠BCE=45°-15°=30°,
∴∠B=30°,
∴∠B=∠BCE,
∴AB∥EC,
即当∠DCB等于15度时,AB∥EC.
∴∠B=180°-90°-60°=30°,
∵AB∥CD,
∴∠DCB=∠B=30°;
(2)DE∥AC,
理由是:∵∠EDC=90°,∠DEC=45°,
∴∠DCE=45°,
∵∠BCA=90°,
∴∠ACE+∠DEC=90°+45°+45°=180°,
∴DE∥AC;
(3)当∠DCB等于15度时,AB∥EC,
理由是:∵∠DCB=15°,∠DCE=45°,
∴∠BCE=45°-15°=30°,
∴∠B=30°,
∴∠B=∠BCE,
∴AB∥EC,
即当∠DCB等于15度时,AB∥EC.
点评:本题考查了平行线的性质和判定,三角形内角和定理的应用,能根据平行线的判定推出两直线平行是解此题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
一条弦把圆分为2:3的两部分,那么这条弦所对的圆周角度数为( )
| A、144° | B、72° |
| C、108° | D、72°或108° |
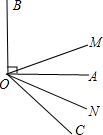 如图,已知∠AOB是直角,ON平分∠AOC,OM平分∠BOC,则∠MON=
如图,已知∠AOB是直角,ON平分∠AOC,OM平分∠BOC,则∠MON=



