Question

【题目】如图，矩形ABCD中，对角线AC与BD相交于点，过点A作AN∥BD，过点B作BN∥AC，两线相交于点N．

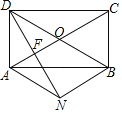
（1）求证：AN＝BN；

（2）连接DN，交AC于点F，若DN⊥NB于点N，求∠DOC的度数．

Answer 1

【答案】（1）见解析；（2）120°

【解析】

（1）根据矩形的性质和已知条件可以证明四边形OANB是平行四边形，进而证明OANB是菱形，即可得结论；
（2）结合（1）可以得∠NDB=30°，进而可求∠DOC的度数．

解：（1）证明：∵矩形ABCD中，对角线AC与BD相交于点O，

∴OA＝OB，

∵AN∥BD，BN∥AC，

∴四边形OANB是平行四边形，

∵OA＝OB，

∴OANB是菱形，

∴AN＝BN，

（2）由（1）可知：

BN＝OB＝OD，

∴BD＝2BN，

∵DN⊥NB，

∴∠DNB＝90°，

∴∠BDN＝30°，

∵BN∥AC，

∴∠DFO＝∠DNB＝90°，

∴∠DOF＝90°﹣30°＝60°，

∴∠DOC＝180°﹣60°＝120°．

答：∠DOC的度数为120°．