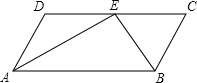
题目内容
【题目】一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的![]() 倍,往返共用
倍,往返共用![]() 小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为
小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为![]() ,两车离开甲地的距离为
,两车离开甲地的距离为![]() ,两车行驶过程中
,两车行驶过程中![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
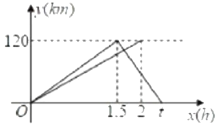
(1)轿车从乙地返回甲地的速度为________![]() ,
,![]() ________;
________;
(2)求轿车从乙地返回甲地时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当轿车从乙地返回甲地的途中与货车相遇时,求相遇处到甲地的距离.
【答案】(1)![]() ,
,![]()
![]() ;(2)
;(2)![]() ;(3)相遇处到甲地的距离为
;(3)相遇处到甲地的距离为![]()
【解析】
(1)首先根据题意求出轿车从甲地到乙地的速度为![]()
![]() ,由此进一步即可求得轿车从乙地返回甲地的速度为
,由此进一步即可求得轿车从乙地返回甲地的速度为![]()
![]() ,从而得出轿车返回时间为,最后进一步计算即可;
,从而得出轿车返回时间为,最后进一步计算即可;
(2)根据题中所给的函数图像以及(1)中的结论,设出一次函数解析式,利用待定系数法求解即可;
(3)首先根据题意求出货车从甲地前往乙地时![]() 与
与![]() 的函数解析式,结合(2)中求出的解析式联立可得方程组,由此进一步求解即可.
的函数解析式,结合(2)中求出的解析式联立可得方程组,由此进一步求解即可.
(1)轿车从甲地到乙地的速度为:![]()
![]() ,
,
∴轿车从乙地返回甲地的速度为![]()
![]() ,
,
∴轿车返回时间为:![]()
![]() ,
,
∴![]()
![]() ,
,
故答案为:![]() ,
,![]()
![]() ;
;
(2)设轿车从乙地返回甲地时![]() 与
与![]() 函数关系式为
函数关系式为![]()
![]() ,
,
∵函数图像过(1.5,120),(2.5,0),
∴![]() ,
,
解得:![]() ,
,
∴轿车从乙地返回甲地时![]() 与
与![]() 函数关系式为
函数关系式为![]() ;
;
(3)设货车从甲地前往乙地时![]() 与
与![]() 的函数解析式为:
的函数解析式为:![]()
![]() ,
,
∵函数图象过点(2,120),
∴![]() ,
,
∴![]() ,
,
即货车从甲地前往乙地时![]() 与
与![]() 的函数解析式为:
的函数解析式为:![]() ,
,
联立轿车从乙地返回甲地时![]() 与
与![]() 函数关系式可得:
函数关系式可得:![]() ,
,
解得:![]()
∴相遇处到甲地的距离为![]() .
.

练习册系列答案
相关题目