Question

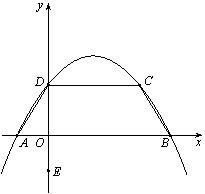
如图，抛物线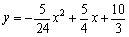交坐标轴于A、B、D三点，过点D作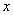轴的平行线交抛物线于点C．直线l过点E（0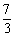，－），且平分梯形ABCD面积．

⑴ 直接写出A、B、D三点的坐标；

⑵ 直接写出直线l的解析式；

⑶ 若点P在直线l上，且在x轴上方，tan∠OPB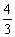＝，求点P的坐标．

 

Answer 1

解：⑴ 点A（－2，0），点B（8，0），点D（0，）；　 

⑵ 直线l：；　 

提示：作CF⊥x轴，F为垂足．先求出矩形OFCD的中心坐标M（3，），则直线ME即为所求直线l．

⑶ 如图，若点P为所求的点，画出△POB的外接圆⊙G，并作GH⊥x轴，H为垂足，则∠OGH＝∠HGB＝∠OPB．

-- ∵　OH＝HB＝4，tan∠OGH＝tan∠HGB＝tan∠OPB＝

-- ∴　GH＝3，GO＝GB＝GP＝5

-- 即⊙G的圆心G坐标为（4，3），半径r＝5　   

-- 将点G坐标代入直线l解析式发现，点G恰巧在直线l上   

-- 设直线l与x轴交于点Q，不难计算GH：QH＝4：3

-- 作PN⊥x轴，GN∥x轴，交于点N，则GN＝3，PN＝4，
因此点P的坐标为（7，7）．