题目内容
14.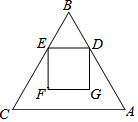 △ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于6$\sqrt{3}$-6.
△ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于6$\sqrt{3}$-6.
分析 如图,作BL⊥AC于L交DE于H,交FG于K.只要证明FG∥AC,求出KL即可解决问题.
解答 解:如图,作BL⊥AC于L交DE于H,交FG于K.
∵△ABC是等边三角形,AC=BC=AB=18,
∴∠B=90°,BL=BC•sin60°=9$\sqrt{3}$,
∵BE=BD,
∴△BED是等边三角形,
∴BE=BD=DE=6,BH=EB•sin60°=3$\sqrt{3}$,
∵HK=EF=6,
∴BK=3$\sqrt{3}$+6,
∴KL=BL-BK=9$\sqrt{3}$-(3$\sqrt{3}$+6)=6$\sqrt{3}$-6,
∵∠BED=∠C=60°,
∴DE∥BC,∵DE∥FG,
∴FG∥AC,
∴点F到AC的距离=6$\sqrt{3}$-6.
故答案为6$\sqrt{3}$-6.
点评 本题考查正方形的性质、等边三角形的判定和性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
4.若点A(a-2,a)在x轴上,则点B(a-1,3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.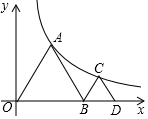 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$+$\sqrt{6}$ | C. | 3$\sqrt{3}$+2$\sqrt{6}$ | D. | 2$\sqrt{6}$ |
9.已知点A(-3,a)、B(-1,b)、C(2,c)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,则且a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
6.-$\sqrt{3}$的相反数为( )
| A. | $\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | 3 | D. | -3 |
 如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式.
如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式. 用5个完全相同的小正方体组合成如图所示的立体图形,它的俯视图为( )
用5个完全相同的小正方体组合成如图所示的立体图形,它的俯视图为( )


