题目内容
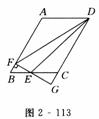
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是⊙O上一点,OD⊥AC,垂足为E,连接BD.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
证明 (1)∵OD⊥AC OD为半径,
 ∴
∴ =
= ,∴∠CBD=∠ABD,
,∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,∴∠OBD=∠ODB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,∴∠OEA=90°,
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°,
又∵AB为⊙O的直径,∴∠ACB=90°,
在Rt△ACB中,BC=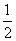 AB,
AB,
∵OD=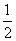 A
A B,∴BC=OD.
B,∴BC=OD.

练习册系列答案
相关题目
 ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥A
ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥A B于F,延长FE与DC的延长线交于点G,设BE=x,△DEF的面积为S.
B于F,延长FE与DC的延长线交于点G,设BE=x,△DEF的面积为S. ;
;
 ,BD=
,BD= ,则AB的长为 ( )
,则AB的长为 ( )
 C.50° D.60°
C.50° D.60°



 剪去
剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )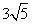 cm
cm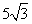 cm
cm