题目内容
 如图,某军港有一雷达站,军舰停泊在雷达站的南偏东60°方向36海里处,另一艘军舰位于军舰的正西方向,与雷达站相距18
如图,某军港有一雷达站,军舰停泊在雷达站的南偏东60°方向36海里处,另一艘军舰位于军舰的正西方向,与雷达站相距18| 2 |
(1)军舰在雷达站的什么方向?
(2)两军舰的距离.(结果保留根号)
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)过点P作PQ⊥MN,交MN的延长线于点Q.在Rt△PQM中求出PQ,进而在Rt△PQN中求出∠QPN;
(2)在Rt△PQM中根据三角函数求出MQ,就得到MN的长.
(2)在Rt△PQM中根据三角函数求出MQ,就得到MN的长.
解答: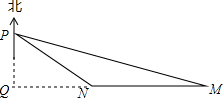 解:过点P作PQ⊥MN,交MN的延长线于点Q.
解:过点P作PQ⊥MN,交MN的延长线于点Q.
(1)在Rt△PQM中,由∠MPQ=60°,
得∠PMQ=30°,又PM=36,
∴PQ=
PM=
×36=18(海里).
在Rt△PQN中,
∵cos∠QPN=
=
=
,
∴∠QPN=45°,即军舰在雷达站的东南方向(或南偏东45°).
答:军舰在雷达站的东南方向.
(2)∵由(1)Rt△PQN为等腰直角三角形,
∴PQ=NQ=18(海里).
在Rt△PQM中,
∵MQ=PQ•tan∠QPM=18•tan60°=18
(海里),
∴MN=MQ-NQ=18
-18(海里).
答:两军舰的距离为(18
-18)海里.
 解:过点P作PQ⊥MN,交MN的延长线于点Q.
解:过点P作PQ⊥MN,交MN的延长线于点Q.(1)在Rt△PQM中,由∠MPQ=60°,
得∠PMQ=30°,又PM=36,
∴PQ=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PQN中,
∵cos∠QPN=
| PQ |
| PN |
| 18 | ||
18
|
| ||
| 2 |
∴∠QPN=45°,即军舰在雷达站的东南方向(或南偏东45°).
答:军舰在雷达站的东南方向.
(2)∵由(1)Rt△PQN为等腰直角三角形,
∴PQ=NQ=18(海里).
在Rt△PQM中,
∵MQ=PQ•tan∠QPM=18•tan60°=18
| 3 |
∴MN=MQ-NQ=18
| 3 |
答:两军舰的距离为(18
| 3 |
点评:本题考查的是解直角三角形的应用-方向角问题,熟知此类问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
已知x1,x2是方程x2-5x-2=0的两个实数根,则x12-x1x2+x22的值为( )
| A、31 | B、29 | C、25 | D、17 |

 在某一电路中,电源电压U保持不变,电流I,电压U,电阻R三者之间满足关系I=
在某一电路中,电源电压U保持不变,电流I,电压U,电阻R三者之间满足关系I= 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.
光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.