题目内容
17.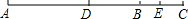 如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E为BC的中点.
如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E为BC的中点.(1)图中共有10条线段;
(2)若BD=9cm,求AC的长;
(3)若DE=10cm,求AC的长.
分析 (1)根据线段的定义解答即可;
(2)根据BC=$\frac{1}{4}$AB,设BC=x,则AB=4x,AC=5x,由于点D为AC的中点,于是得到CD=$\frac{1}{2}$AC=$\frac{5}{2}$x,列方程即可得到结果;
(3)根据BC=$\frac{1}{4}$AB,设BC=x,则AB=4x,AC=5x,由于点D为AC的中点,于是得到CD=$\frac{1}{2}$AC=$\frac{5}{2}$x,根据点E为BC的中点,证得BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$x,列方程即可得到结论.
解答 解:(1)图中共有10条线段;
故答案为:10;
(2)∵BC=$\frac{1}{4}$AB,
∴设BC=x,则AB=4x,AC=5x,
∵点D为AC的中点,
∴CD=$\frac{1}{2}$AC=$\frac{5}{2}$x,
∴BD=CD-BC=$\frac{5}{2}$x-x=9,
∴x=6,
∴AC=30cm;
(3)∵BC=$\frac{1}{4}$AB,
∴设BC=x,则AB=4x,AC=5x,
∵点D为AC的中点,
∴CD=$\frac{1}{2}$AC=$\frac{5}{2}$x,
∵点E为BC的中点,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$x,
∴DE=CD-CE=$\frac{5}{2}$x-$\frac{1}{2}$x=10,
∴x=5,
∴AC=25cm.
点评 本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.会利用代数法解决求线段长的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些土豆后,又降价出售,售出土豆的千克数与他手中持有钱数(含备用零钱)的关系如图所示,结合图象回答下列问题.
一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些土豆后,又降价出售,售出土豆的千克数与他手中持有钱数(含备用零钱)的关系如图所示,结合图象回答下列问题.