题目内容
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在(0,-1)的下方,与x轴的交点为(x1,0)和(x2,0),其对称轴为直线x=1,则下列结论错误的是( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在(0,-1)的下方,与x轴的交点为(x1,0)和(x2,0),其对称轴为直线x=1,则下列结论错误的是( )| A、abc>0 | ||
| B、3<x2<4 | ||
C、a>
| ||
| D、b2-4ac<4a |
考点:抛物线与x轴的交点,二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:A、根据图示知,抛物线开口方向向上,则a>0,抛物线的对称轴x=-
=1>0,则b<0,抛物线与y轴交与负半轴,则c<0,所以abc>0,故本选项正确;
B、∵-2<x1<-1,对称轴为直线x=1,∴3<x2<4,故本选项正确;
C、∵当x=-2时,y>0,
∴4a-2b+c>0,
∵x=-
=1,
∴b=-2a,
∴8a+c>0,
∴a>-
,
∵c<-1,
∴-
>
,
∴a>
;
故本选项正确;
D、∵二次函数y=ax2+bx+c的图象与y轴的交点在(0,-1)的下方,对称轴在y轴右侧,a>0,
∴最小值:
<-1,
∴4ac-b2<-4a,
∴b2-4ac>4a,故本选项错误.
故选D.
| b |
| 2a |
B、∵-2<x1<-1,对称轴为直线x=1,∴3<x2<4,故本选项正确;
C、∵当x=-2时,y>0,
∴4a-2b+c>0,
∵x=-
| b |
| 2a |
∴b=-2a,
∴8a+c>0,
∴a>-
| c |
| 8 |
∵c<-1,
∴-
| c |
| 8 |
| 1 |
| 8 |
∴a>
| 1 |
| 8 |
故本选项正确;
D、∵二次函数y=ax2+bx+c的图象与y轴的交点在(0,-1)的下方,对称轴在y轴右侧,a>0,
∴最小值:
| 4ac-b2 |
| 4a |
∴4ac-b2<-4a,
∴b2-4ac>4a,故本选项错误.
故选D.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
“春运”期间,连续7天去某车站对旅客人数进行统计,每天旅客的人数统计如下表:其中众数和中位数分别是( )
| 日期(2014年1月) | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 | 27日 |
| 人数(单位:万) | 1.2 | 2 | 2.5 | 2 | 1.2 | 2 | 0.6 |
| A、1.2,2 |
| B、2,2.5 |
| C、2,2 |
| D、1.2,2.5 |
在下列各数中,是无理数的是( )
| A、2π | ||
B、
| ||
| C、3.14 | ||
D、
|
一元一次方程2x-4=0的解是( )
| A、x=1 | B、x=2 |
| C、x=3 | D、x=4 |
一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,求这张卡片与口袋外的两张卡片上的数作为三角形三边的长,能构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
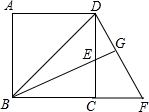 如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F.
如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F.