题目内容
13. 如图,△ABC和△DEC均为等边三角形,∠DAB=40°,∠ACD=15°,则∠BEC的度数为( )
如图,△ABC和△DEC均为等边三角形,∠DAB=40°,∠ACD=15°,则∠BEC的度数为( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
分析 由等边三角形的性质得出AC=BC,CE=CD,∠BAC=∠ACB=∠ECD=60°,求出∠ACD=∠BCE=15°,由SAS证明△ACD≌△BCE,得出∠EBC=∠CAD=20°,由三角形内角和定理即可得出∠BEC的度数.
解答 解:∵△ABC和△DEC都是等边三角形,
∴AC=BC,CE=CD,∠BAC=∠ACB=∠ECD=60°,
又∵∠ACB=∠ACD+∠BCD,∠ECD=∠BCE+∠BCD,
∴∠ACD=∠BCE=15°,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACD=∠BCE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠EBC=∠CAD=∠BAC-∠DAB=60°-40°=20°,
∴∠BEC=180°-∠EBC-∠BCE=145°.
故选:D.
点评 本题主要考查了等边三角形的性质、全等三角形的判定及性质、三角形内角和定理;熟练掌握等边三角形的性质,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
8.如图是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
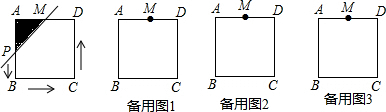
 如图,点P为长方形ABCD周长上的一个动点,它以每秒1厘米的速度从A点出发沿顺时针方向运动.
如图,点P为长方形ABCD周长上的一个动点,它以每秒1厘米的速度从A点出发沿顺时针方向运动. 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度为每秒1个单位长度,当Q点运动到A点,P、Q两点同时停止运动,设点Q运动的时间为t秒.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度为每秒1个单位长度,当Q点运动到A点,P、Q两点同时停止运动,设点Q运动的时间为t秒.