Question

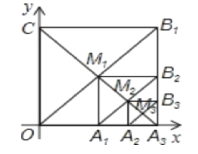
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;..依此类推,这样作的第6个正方形对角线交点的坐标为____.

Answer 1

【答案】

【解析】

根据正方形的性质得到OM1=M1A1，∠OM1A1=90°，设OM1=M1A1=x，由勾股定理得到方程x2+x2=12，解方程求出x的值，同理可以求出其它正方形的边长，依此类推可求出A6A7=A7M6=，计算出OA7的长度，即可得到答案.

正方形OA1B1C，

∴OM1=M1A1,∠OM1A1=90°，

设OM1=M1A1=x，

由勾股定理得：x2+x2=12，

解得：x=，

同理可求出OA2=A2M1= ，

A2M2=,A2A3=,…A6A7=A7M6=，

∴OA7=1.

故答案为：.