Question

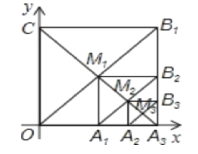
【题目】如图，点、的坐标分别为，，直线与轴交于点、与轴交于点.

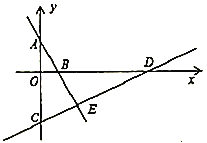
（1）直线解析式为，求直线与交点的坐标；

（2）四边形的面积是________；

（3）求证：.

Answer 1

【答案】（1） （2）4 （3）证明见解析

【解析】

（1）运用待定系数法即可得到直线AB解析式，再根据方程组的解，即可得到直线AB与CD交点E的坐标；

（2）根据坐标轴上点的特征求出C、D两点的坐标，然后根据面积公式计算即可；

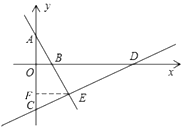
（3）作EF⊥y轴于点F，根据勾股定理分别求出，利用勾股定理的逆定理判断即可．

解：（1）点、的坐标分别为，，

∴，解得，

故直线的解析式是，

则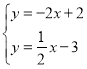，解得

∴；

（2直线CD的解析式为，

当x=0时，y=-3，当y=0时，x=6，

则点C的坐标是（0，-3），点D的坐标是（6，0）.

==4；

（3）作轴于点，

由，，

∴，，，

，

，

，

∴，

∴是直角三角形，且

∴.