题目内容
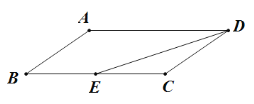
【题目】如图，在□ABCD中，AB=3，AD=6，
，E为BC的中点，
（1）求
；
（2）求DE的边长.
【答案】（1）30°；（2）
【解析】
(1)由平行四边形的性质、中点的性质求出EC=CD，根据∠BCD求出
；
（2）作CF⊥ED，利用三角函数求出EF的长度即可知DE的长.
（1）∵四边形ABCD是平行四边形，
∴BC=AD=6，CD=AB=3，∠ABC+∠C=180°,
∵
∴∠BCD=120°，
∵E为BC的中点，
∴EC=CD=3,
∴△ECD是等腰三角形，
∵∠ECD=120°，EC=ED,
∴∠CED=
（2）作CF⊥ED，垂足为F
在Rt△CEF中，∠CFE=90°，EC=3，∠CED=30°，
∴EF=EC×cos30°=
,
∴DE=2EF=.
练习册系列答案
阅读快车系列答案
相关题目
