题目内容
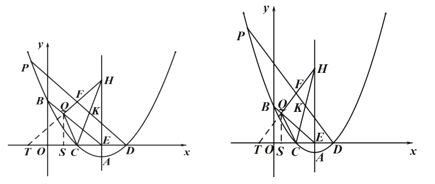
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,过抛物线的顶点
,过抛物线的顶点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为点
,垂足为点![]() ,作直线
,作直线![]() .
.
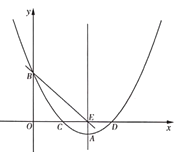
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为第一象限内直线
为第一象限内直线![]() 上的一点,连接
上的一点,连接![]() ,取
,取![]() 的中点
的中点![]() ,作射线
,作射线![]() 交抛物线于点
交抛物线于点![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,在线段![]() 上有一点
上有一点![]() ,连接
,连接![]() ,
,![]() ,线段
,线段![]() 交线段
交线段![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)直线![]() 的解析式为
的解析式为![]() .(2)
.(2)![]() .(3)
.(3)![]() 或
或![]()
【解析】
(1)根据抛物线可得对称轴,可知点E的坐标,利用待定系数法可得一次函数BE的解析式;
(2)如图,作辅助线,构建直角三角形,根据抛物线过点![]() ,可得a的值,计算y=0时,x的值可得C和D两点的坐标,从而知CD的值,根据P的横坐标可表示其纵坐标,根据
,可得a的值,计算y=0时,x的值可得C和D两点的坐标,从而知CD的值,根据P的横坐标可表示其纵坐标,根据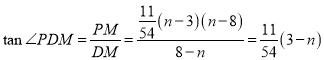 ,
,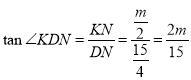 ,列方程为
,列方程为![]() ,可得结论;
,可得结论;
(3)如图,延长HF交x轴于T,先根据已知得∠FDO=∠FTO,由等角的三角函数相等和(2)中的结论得:tan∠FDO=tan∠FTO,则![]() ,可得ET和CT的长,令∠FDO=∠FTO=2α,表示角可得∠TCQ=∠TQC,则TQ=CT=5,
,可得ET和CT的长,令∠FDO=∠FTO=2α,表示角可得∠TCQ=∠TQC,则TQ=CT=5,
设Q的坐标为![]() ,根据定理列方程可得:TS2+QS2=TQ2,
,根据定理列方程可得:TS2+QS2=TQ2,![]() ,解得
,解得![]() ,
,![]() ;根据两个t的值分别求n的值即可.
;根据两个t的值分别求n的值即可.
解:(1)抛物线的对称轴为![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则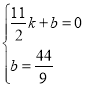 ,解得:
,解得: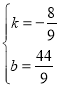 ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
(2)如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵抛物线![]() 经过
经过![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,∴点
上,∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴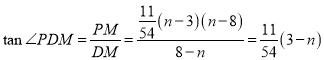 ,
,
∵![]() 轴,∴
轴,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,在
,在![]() 中,
中,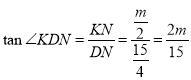 .
.
∴![]() ,
,
∴![]() .
.
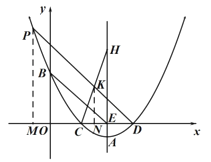
(3)如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,令
,令![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 在直线
在直线![]() 上,∴可设
上,∴可设![]() 的坐标为
的坐标为![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
解得![]() ,
,![]() .
.
①如图2,当![]() 时,
时,![]() ,
,![]() ,
,
在![]() 中,
中,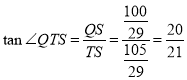 ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
②如图3,当![]() 时,
时,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.