Question

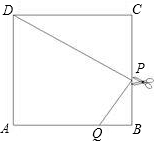如图，边长为3的正方形纸片ABCD，用剪刀沿PD剪下Rt△PCD，其中∠PDC=30°．
（1）求PC的长；
（2）若从余料（梯形ABPD）再剪下另一个Rt△PBQ，使点Q在AB上，则当QB的长为多少时，△PBQ∽△DCP？

Answer 1

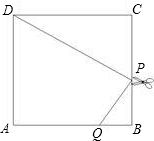解：（1）法一：在Rt△PCD中，∠C=90°，∠PDC=30°，CD=3，
∵tan∠PDC=，
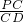∴PC=CD•tan∠PDC=3×=．

法二：∵四边形ABCD为正方形，
∴∠C=90°，
又∵∠PDC=30°，
∴PD=2PC，
设PC=x，则PD=2x，
在Rt△PCD中，由勾股定理得PC²+CD²=PD²x²+3²=（2x）²，
解得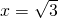（舍去负值），
∴PC=．

（2）法一：由（1）可知，PC=．
∴PB=BC-PC=3-，
又由正方形ABCD可得∠B=∠C=90°，
∴当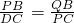时，△PBQ∽△DCP，
由，
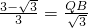解得QB=-1，
∴当QB=-1，时，△PBQ∽△DCP．
法二：由（1）可知，PC=．
∴PB=BC-PC=3-，
∵∠B=∠C=90°，
∴要使△PBQ∽△DCP，则必须有∠BPQ=∠CDP=30°，
在Rt△PBQ中，由tan∠BPQ=，可得
QB=BPtan∠BPQ=（3-）×=-1，
故当QB=-1时，△PBQ∽△DCP．
答：（1）PC的长为；
（2）当QB的长为-1时，△PBQ∽△DCP．
分析：（1）此题有两种解法，法一：根据在Rt△PCD中，∠C=90°，∠PDC=30°，CD=3，利用锐角三角函数值即可求得答案．
法二：根据四边形ABCD为正方形，∠C=90等已知条件求证PD=2PC，再设PC=x，利用勾股定理即可求得PC，
（2）此题有两种解法，由（1）和由正方形ABCD可得∠B=∠C=90°根据当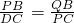时△PBQ∽△DCP，可求出QB．
法二：由（1）可知，PC=，可得BP，要使△PBQ∽△DCP，则必须有∠BPQ=∠CDP=30°再由tan∠BPQ=可求得QB．
点评：此题主要考查相似三角形的判定与性质，正方形的性质，解直角三角形等知识点，综合性强，有一定的拔高难度，利于学生系统的掌握知识．