题目内容
17.不等式x+5≥2的解在数轴上表示为( )| A. |  | B. |  | C. |  | D. |  |
分析 移项、合并得不等式解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则判断即可得.
解答 解:移项,得:x≥2-5,
合并,得:x≥-3,
故选:C.
点评 本题主要考查解一元一次不等式的基本能力,熟练掌握“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则是关键.

练习册系列答案
相关题目
7.已知某品牌的饮料有大瓶和小瓶装之分,某超市花了3800元购进一批该品牌的饮料共1000瓶,其中,大瓶和小瓶饮料的进价及售价如表所示.
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次购买大瓶饮料时,每满2瓶就送1瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次购买大瓶饮料时,每满2瓶就送1瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
| 大瓶 | 小瓶 | |
| 进价(元/瓶) | 5 | 2 |
| 售价(元/瓶) | 7 | 3 |
5.要使二次根式$\sqrt{3-m}$有意义,则m的取值范围为( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
6.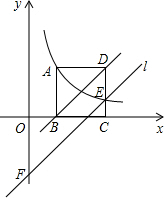 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )| A. | (0,-$\frac{7}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,-3) | D. | (0,-$\frac{10}{3}$) |
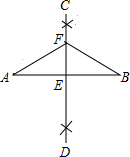 如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.
如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.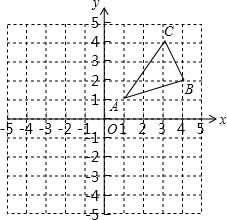 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)