��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=-![]() x2+bx+c��x����A��B���㣬��y���ڵ�C,ֱ��y=x+6����A��C���㣮
x2+bx+c��x����A��B���㣬��y���ڵ�C,ֱ��y=x+6����A��C���㣮
��1���������ߵĽ���ʽ��
��2����P�ǵڶ������������ϵ�һ�����㣬����P��PQ��AC,PQ��ֱ��BC�ڵ�Q�����P�ĺ�����Ϊt����Q�ĺ�����Ϊm,��m��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����P����ֱ��AC�ĶԳƵ��K,����QK,����K����ֱ��y=-![]() x��ʱ�����߶�QK�ij�.
x��ʱ�����߶�QK�ij�.



���𰸡�(1) y=-![]() x2-x+6����2��m=
x2-x+6����2��m=![]() t2+
t2+![]() t����3��
t����3��![]() .
.
���������������:(1)�ȸ���һ�κ������A,C������,Ȼ���A,C������κ�������ʽ�ⷽ���鼴��������κ�������ʽ,(2)����PQ��AC,��ɵ�PQ����ֱ�߽���ʽ�е�k,����P������ɱ�ʾPQ��ֱ�߽���ʽ,Ȼ��������PQ��BC�������,(3)�ȸ��ݵ�P����ֱ��AC�ĶԳƵ�K,�����е����깫ʽ��ʾ����K,Ȼ�����ֱ��y=��![]() x,�������K,Ȼ������������빫ʽ�����QK.
x,�������K,Ȼ������������빫ʽ�����QK.
�������:(1) ��Ϊֱ��y=x+6����A,C����,
����A(��6,0),C(0,6),
��Ϊ������y=![]() x2+bx+c����A,C����,��A(��6,0),C(0,6)����ɵ�:
x2+bx+c����A,C����,��A(��6,0),C(0,6)����ɵ�:
 ,
,
���: ![]() ,
,
���Զ��κ�������ʽΪ: ![]() ,
,
(2)��ΪP������������,����P��������(t, ![]() ),Q����ֱ��BC��,
),Q����ֱ��BC��,
��ֱ��BC�Ľ���ʽΪy=kx+b,��������ɵ�:
![]() ,���:
,���: ![]() ,
,
����ֱ��BC�Ľ���ʽΪ: y=��2x+6,
��ΪPQ��AC,
���Կɵ�Ϊ: ![]() ���:
���: ![]() ,
,
����ֱ��PQ��ֱ�߽���ʽΪ: y=x+![]() ,
,
��ֱ��PQ��ֱ��BC���������Q�ĺ�����:
��2x+6= x+![]() ,
,
��3x=![]() ,
,
x= ![]() ,
,
����m= ![]() ,
,
(3)��������ɵ�:ֱ��QK��ֱ��AC��ֱ,�ɵ�:
![]() ,���:
,���: ![]()
����ֱ��QK�Ľ���ʽΪ: y=��x+![]() ,
,
����ֱ��QK��ֱ��AC,�������ֱ�ߵĽ��������:
��x+![]() = x+6,
= x+6,
���: x=![]() ,
,
���Խ���������Ϊ: y=![]() ,
,
�����е����깫ʽ�ɵ�K������Ϊ(![]() ,
,![]() ),
),
��ΪK��y=��![]() x��,
x��,
����![]() ,���:
,���:
��ΪQ������Ϊ(![]() ,
,![]() ), K������Ϊ(
), K������Ϊ(![]() ,
,![]() ),
),
��������֮����빫ʽ�ɵ�:
QK=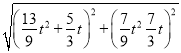 =
=![]() .
.
�㾦:������Ҫ������κ���ͼ������,һ�κ���ͼ������,�������Ĺؼ����ܹ��ô���ϵ�������һ�κ�������ʽ,���������κ�������ʽ�����Ľ����ǽ������Ĺؼ�.

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�





