题目内容
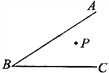
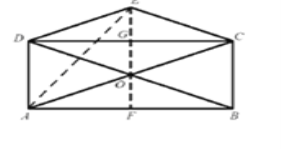
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,若
,若![]() ,
, ![]() .
.
①求![]() 的值;
的值;
②若点![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,再以
,再以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,到达点
,到达点![]() 后停止运动.当点
后停止运动.当点![]() 沿上述路线运动到点
沿上述路线运动到点![]() 所需要的时间最短时,求
所需要的时间最短时,求![]() 的长和点
的长和点![]() 走完全程所需的时间.
走完全程所需的时间.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 和
和![]() 走完全程所需时间为
走完全程所需时间为![]() .
.
【解析】试题分析:(1)利用四边相等的四边形是菱形进行证明即可;
(2)①构造直角三角形求![]() 即可;
即可;
②先确定点![]() 沿上述路线运动到点
沿上述路线运动到点![]() 所需要的时间最短时的位置,再计算运到的时间.
所需要的时间最短时的位置,再计算运到的时间.
试题解析:(1)![]() 四边形
四边形![]() 是矩形,
是矩形, ![]() ,
,
![]() 与
与![]() 交于点O,且
交于点O,且![]() 关于
关于![]() 对称,
对称,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形;
是菱形;
(2)①连接![]() ,直线
,直线![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
![]() 关于
关于![]() 的对称图形为
的对称图形为![]() ,
,
![]()
![]() ,
,
![]() 在矩形
在矩形![]() 中,
中, ![]() 为
为![]() 的中点,且O为AC的中点,
的中点,且O为AC的中点,
![]() 为
为![]() 的中位线 ,
的中位线 , ![]() ,
,
同理可得: ![]() 为
为![]() 的中点,
的中点, ![]() ,
,
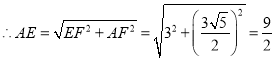 ,
,
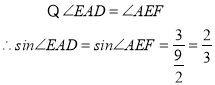 ;
;
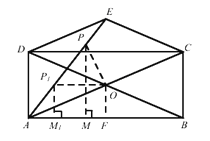
②过点P作![]() 交
交![]() 于点
于点![]() ,
,
![]() 由
由![]() 运动到
运动到![]() 所需的时间为3s,
所需的时间为3s,
![]() 由①可得,
由①可得, ![]() ,
,
![]() 点O以
点O以![]() 的速度从P到A所需的时间等于以
的速度从P到A所需的时间等于以 ![]() 从M运动到A,
从M运动到A,
即: ![]() ,
,
![]() 由O运动到P所需的时间就是OP+MA和最小.
由O运动到P所需的时间就是OP+MA和最小.
![]() 如下图,当P运动到
如下图,当P运动到![]() ,即
,即![]() 时,所用时间最短.
时,所用时间最短.
![]() ,
,
![]() 在
在![]() 中,设
中,设![]() ,
, ![]() ,
,
![]() ,
,
解得: ![]() ,
, ![]() ,
,
![]() 和
和![]() 走完全程所需时间为
走完全程所需时间为![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】已知下表:
x | 0 | 1 | 2 |
ax2 | 1 | ||
ax2+bx+c | 3 | 3 |
(1)求a、b、c的值,并在表内空格处填入正确的数;
(2)请你根据上面的结果判断:
①是否存在实数x,使二次三项式ax2+bx+c的值为0?若存在,求出这个实数值;若不存在,请说明理由.
②画出函数y=ax2+bx+c的图象示意图,由图象确定,当x取什么实数时,ax2+ bx+c>0?