Question

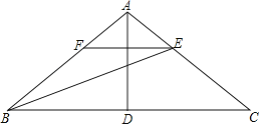
【题目】如图,在不等边中,,垂足为M,,垂足为N,且,点Q在AC上,,下列结论：

,

,

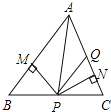
平分,

平分,

≌,其中正确的个数有()

A. 5个B. 4个C. 3个D. 2个

Answer 1

【答案】B

【解析】

利用“HL”证明△APM和△APN全等，根据全等三角形的性质可得：AN＝AM，∠PAM＝∠PAN，∠APM＝∠APN，再根据等边对等角可得∠PAN＝∠APQ，从而得到∠PAM＝∠APQ，然后根据内错角相等，两直线平行可得QP∥AM，故①②③④正确；而条件不足，无法证明△BMP≌△CNP，故⑤错误．

解：∵PM⊥AB，PN⊥AC，

∴∠AMP＝∠ANP＝90°，

在Rt△APM和Rt△APN中，，

∴Rt△APM≌Rt△APN（HL），

∴AN＝AM，∠PAM＝∠PAN，∠APM＝∠APN，

∵PQ＝QA，

∴∠PAN＝∠APQ，

∴∠PAM＝∠APQ，

∴QP∥AM，故①②③④正确；

条件不足，无法证明△BMP≌△CNP，故⑤错误．

综上所述，正确的有4个，

故选：B．