题目内容
 15、如图,把含30°的直角三角板ABC绕直角顶点B顺时钟旋转到△DBE的位置,AC交BD于点G,BC交DE于点F,若∠BFE=85°,则∠AGD的度数是
15、如图,把含30°的直角三角板ABC绕直角顶点B顺时钟旋转到△DBE的位置,AC交BD于点G,BC交DE于点F,若∠BFE=85°,则∠AGD的度数是65°
.分析:首先根据三角形的内角和定理,在△BEF中,求得∠CBE的度数,然后由旋转的性质,求得∠ABD的度数,又由三角形外角的性质可得∠AGD=∠A+∠ABD,即可求得∠AGD的度数.
解答:解:根据题意可得:∠A=∠D=30°,∠C=∠E=60°,
∵∠BFE=85°,∠BFE+∠E+∠CBE=180°,
∴∠CBE=180°-85°-60°=35°,
根据旋转的性质可得:∠ABD=∠CBE=35°,
∴∠AGD=∠A+∠ABD=30°+35°=65°.
故答案为:65°.
∵∠BFE=85°,∠BFE+∠E+∠CBE=180°,
∴∠CBE=180°-85°-60°=35°,
根据旋转的性质可得:∠ABD=∠CBE=35°,
∴∠AGD=∠A+∠ABD=30°+35°=65°.
故答案为:65°.
点评:此题考查了旋转的性质,三角形内角和定理以及三角形外角的性质.此题比较简单,解题的关键是注意数形结合思想的应用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
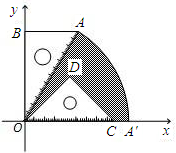 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.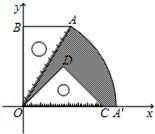 已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,
已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中, (2012•南平模拟)如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且
(2012•南平模拟)如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且 如图,把含30°的直角三角板ABC绕直角顶点B顺时钟旋转到△DBE的位置,AC交BD于点G,BC交DE于点F,若∠BFE=85°,则∠AGD的度数是________.
如图,把含30°的直角三角板ABC绕直角顶点B顺时钟旋转到△DBE的位置,AC交BD于点G,BC交DE于点F,若∠BFE=85°,则∠AGD的度数是________.