题目内容
11.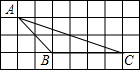 如图所示,在4×8的矩形网格中,每个小正方形的边长都为1,△ABC的三个顶点都在格点上,则tan∠BAC的值为$\frac{1}{2}$.
如图所示,在4×8的矩形网格中,每个小正方形的边长都为1,△ABC的三个顶点都在格点上,则tan∠BAC的值为$\frac{1}{2}$.
分析 作BD⊥AC于D,则∠BDA=90°,由勾股定理求出AB、AC,由△ABC的面积求出BD,根据勾股定理求出AD,在Rt△ABD中,即可求出tan∠BAC的值.
解答 解:作BD⊥AC于D,如图所示: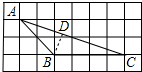 则∠BDA=90°,
则∠BDA=90°,
根据勾股定理得:AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
∵△ABC的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4×2,
∴BD=$\frac{8}{2\sqrt{10}}$=$\frac{2\sqrt{10}}{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{8-\frac{8}{5}}$=$\frac{4\sqrt{10}}{5}$,
∴tan∠BAC=$\frac{BD}{AD}$=$\frac{\frac{2\sqrt{10}}{5}}{\frac{4\sqrt{10}}{5}}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 本题考查了勾股定理、锐角三角函数、三角形面积的计算;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
6.当x=1时,代数式x3+x+m的值是7,则当x=-1时,这个代数式的值是( )
| A. | 7 | B. | 3 | C. | 1 | D. | -7 |
16.若(x-1)3=a3x3+a2x2+a1x+a0,那么a3+a2+a1=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.已知多项式x2+3x=3,可求得另一个多项式3x2+9x-4的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
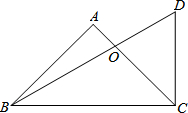 一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.
一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.