题目内容
8. 如图,已知∠AOB是平角,∠AOC=20°,∠COD:∠DOB=3:13,且OE平分∠BOD,求∠COE的度数.
如图,已知∠AOB是平角,∠AOC=20°,∠COD:∠DOB=3:13,且OE平分∠BOD,求∠COE的度数.
分析 根据题意分别求出∠COD和∠DOE即可解决问题.
解答 解:∵∠AOB是平角,∠AOC=20°,
∴∠BOC=180°-20°=160°,
即∠COD+∠DOB=160°,
又∵∠COD:∠DOB=3:13,
∴∠COD=$\frac{3}{16}$∠COD=$\frac{3}{16}$×160°=30°,∠DOB=$\frac{13}{16}$×160°=130°,
∵OE平分∠BOD
∴∠DOE=$\frac{1}{2}$∠BOD=65°,
∴∠COE=∠COD+∠DOE=30°+65°=95°.
点评 本题考查角的计算、角平分线的定义等知识,解题的关键是灵活运用所学知识,熟练掌握角的和差定义解决问题,属于中考常考题型.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.计算(-2)×3的结果是( )
| A. | -5 | B. | -6 | C. | 1 | D. | 6 |
16.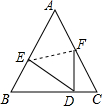 如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则$\frac{AE}{AF}$的值等于( )
如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则$\frac{AE}{AF}$的值等于( )
 如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则$\frac{AE}{AF}$的值等于( )
如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则$\frac{AE}{AF}$的值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}+1}}{3}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
1.海南省某种植园收获香蕉20000千克,其中香牙蕉12000千克、黄帝蕉8000千克,准备运往海口与文昌销售;根据市场供需,海口需要香蕉15000千克,文昌需要香蕉5000千克,海口与文昌两地的香蕉售价如下表所示:
(1)若该种植园供应海口市的香牙蕉与黄帝蕉的比是2:1,请问该种植园供应文昌市的香牙蕉与黄帝蕉各是多少千克?
(2)若海口与文昌的香蕉都能在保质期内销售完,请你设计一种销售方案,使销售的收入最大,并估算出获得的最大销售收入.
| 价格 品种 地区 | 黄帝蕉 (元/千克) | 香牙蕉 (元/千克) |
| 海口 | 5 | 4.8 |
| 文昌 | 4.2 | 3.6 |
(2)若海口与文昌的香蕉都能在保质期内销售完,请你设计一种销售方案,使销售的收入最大,并估算出获得的最大销售收入.
 如图:列车6258次从福利屯到佳木斯途经笔架山、丰乐镇、太平镇、四马架四个停靠车站,两站之间的距离各不相同,则福利屯至佳木斯和沿途车站售票员应共准备单程15种火车票(假设没有异地售票).
如图:列车6258次从福利屯到佳木斯途经笔架山、丰乐镇、太平镇、四马架四个停靠车站,两站之间的距离各不相同,则福利屯至佳木斯和沿途车站售票员应共准备单程15种火车票(假设没有异地售票). 如图,矩形ABCD由3*4个小正方形组成,此图中不是正方形的矩形有40个.
如图,矩形ABCD由3*4个小正方形组成,此图中不是正方形的矩形有40个. 如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°.
如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°.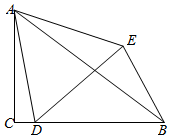 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.