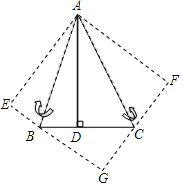
题目内容
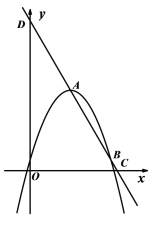
【题目】如图,抛物线交![]() 轴于
轴于![]() ,
,![]() ,交
,交![]() 轴于
轴于![]() .
.
(1)求抛物线解析式;
(2)点![]() 在第一象限的抛物线上,
在第一象限的抛物线上,![]() 与
与![]() 的面积比为
的面积比为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,在点![]() 与
与![]() 之间的抛物线上取点
之间的抛物线上取点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 轴于
轴于![]() 、交
、交![]() 延长线于
延长线于![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设抛物线解析式为![]() ,用待定系数法求抛物线解析式即可;
,用待定系数法求抛物线解析式即可;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,利用三角形的面积比推出
,利用三角形的面积比推出![]() ,设
,设![]() ,代入抛物线解析式即可得出m的值,从而得出点D的坐标;
,代入抛物线解析式即可得出m的值,从而得出点D的坐标;
(3)过点![]() 作
作![]() ,推出
,推出![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,推出
,推出![]() ,再作
,再作![]() ,
,![]() ,可证明
,可证明![]() ,设
,设![]() ,得出
,得出![]() ,
,![]() ,再推出
,再推出![]() 为等腰三角形,进一步推出点E的坐标.
为等腰三角形,进一步推出点E的坐标.
解:(1)设抛物线解析式为![]()
将![]() ,
,![]() ,
,![]()
代入![]() 中
中
![]() ,
,![]() ,
,![]()
![]()
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]()
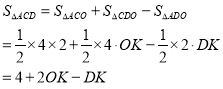
![]()
![]()
∴![]()
设![]() 代入
代入![]()
![]()
![]()
![]() ,
,![]()
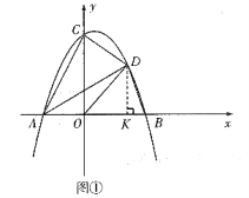
(3)![]() ,
,![]()
过点![]() 作
作![]()
![]()
![]()
![]()
过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]()
![]()
![]()
![]()
![]()
![]()
作![]() ,
,![]()
![]()
![]()
设![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() 为等腰三角形
为等腰三角形
![]()
![]() ,
,![]() 或
或![]()
![]() 在第一象限
在第一象限
![]()

练习册系列答案
相关题目
【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.