题目内容
1.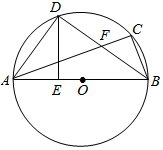 如图,△ABC内接于⊙O,AB为直径,点D是$\widehat{AC}$上一点,且∠DAC=∠DBA,过点D作DE⊥AB,垂足为点E,连结AD.
如图,△ABC内接于⊙O,AB为直径,点D是$\widehat{AC}$上一点,且∠DAC=∠DBA,过点D作DE⊥AB,垂足为点E,连结AD.(1)求证:DB平分∠CBA;
(2)连接CD,若CD=5,BD=12,求⊙O的半径.
分析 (1)根据圆周角定理即可得到结论;
(2)连接CD,由∠CBD=∠DBA,得到CD=AD,根据AB为直径,得到∠ADB=90°,根据勾股定理即可得到结论.
解答 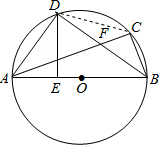 (1)证明:∵∠DAC=∠DBC,∠DAC=∠DBA,
(1)证明:∵∠DAC=∠DBC,∠DAC=∠DBA,
∴∠DBA=∠CBD,
∴DB平分∠CBA;
(2)解:连接CD,
∵∠CBD=∠DBA,
∴$\widehat{AD}$=$\widehat{CD}$,
∴CD=AD,
∵CD﹦5,
∴AD=5,
∵AB为直径,
∴∠ADB=90°,
∵BD=12,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=13,
故⊙O的半径为6.5.
点评 此题主要考查了圆周角定理和勾股定理,熟练利用圆周角定理得出各等量关系是解题关键.

练习册系列答案
相关题目
12.某果农种了50棵苹果树,收获时,他把苹果树的产量做了一下统计,得到下表:
(1)苹果产量的众数是35千克;中位数是35千克;平均数是35千克;
(2)市场上苹果的销售价为8元/千克,化肥、农药、人工费等共投入资金1000元,则今年该果农纯收入多少元?
| 质量(千克) | 33 | 34 | 35 | 36 | 38 |
| 数量(棵) | 10 | 5 | 20 | 10 | 5 |
(2)市场上苹果的销售价为8元/千克,化肥、农药、人工费等共投入资金1000元,则今年该果农纯收入多少元?
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{\frac{1}{3}}$ |
10.下列图形中,不是中心对称图形但是轴对称图形的是( )
| A. |  等腰三角形 | B. |  平行四边形 | C. |  矩形 | D. |  菱形 |