题目内容
1.已知$\frac{a-b}{b}$=$\frac{2}{3}$,求:(1)$\frac{a}{b-3a}$;(2)$\frac{3a+2b}{2a-3b}$.分析 先利用内项之积等于外项之积得到3a-3b=2b,则b=$\frac{3}{5}$a,然后把b=$\frac{3}{5}$a分别代入(1)、(2)的代数式中进行分式的运算即可.
解答 解:∵$\frac{a-b}{b}$=$\frac{2}{3}$,
∴3a-3b=2b,
∴b=$\frac{3}{5}$a,
(1)原式=$\frac{a}{\frac{3}{5}a-3a}$=-$\frac{5}{12}$;
(2)原式=$\frac{3a+\frac{6}{5}a}{2a-\frac{9}{5}a}$=21.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
11.绝对值大于2且小于5的所有整数的积是( )
| A. | -144 | B. | 144 | C. | 0 | D. | 7 |
9.($\frac{2}{3}$)2014•(-1.5)2015=( )
| A. | ($\frac{2}{3}$)2014 | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | (-$\frac{3}{2}$)2014 |
6.已知$\frac{2a}{3b+3c}$=$\frac{2b}{3c+3a}$=$\frac{2c}{3a+3b}$=k,则k的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$或-$\frac{2}{3}$ | D. | $\frac{2}{3}$或-1 |
13.下列各组单项式中,不是同类项的是( )
| A. | 3与-2 | B. | -xy与yx | C. | $\frac{1}{3}$a与$\frac{1}{2}$b | D. | $\frac{1}{3}$x2y与$\frac{2}{3}$yx2 |
11.某自行车厂一局计划生产1400辆自行车,平均每天生产200辆,由于各种原因,实际上每天的生产量与计划量相比有出入,如表是某周的生产情况(实际上每天的生产量比计划量增产记为正,实际上每天的生产量比计划量减产记为负):
(1)根据记录可知,将这一周的每天生产填入表
(2)该厂实行计件工资制,若能完成每天计划的生产量,每生产一辆得60元,增产部分按每辆80元计算,如果不能完成每天计划的生产量,则每天生产一辆得50元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -10 | +8 | -4 | +10 | +2 | +6 | -6 |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 每天生产量(辆) | 190 | 208 | 196 | 210 | 202 | 206 | 194 |
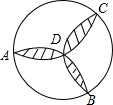 小明把如图所示的圆形纸板(点A,B,C是圆的三等分点)挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则投中阴影区域的概率是1-$\frac{3\sqrt{3}}{2π}$.
小明把如图所示的圆形纸板(点A,B,C是圆的三等分点)挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则投中阴影区域的概率是1-$\frac{3\sqrt{3}}{2π}$.