题目内容
经过点A(-4,5)的抛物线y=-x2+bx+5与y轴交于点B.点M在抛物线的对称轴上,点N在抛物线上,且以A,B,M,N为顶点的四边形是平行四边形.则点N的坐标为________.
(2,-7),(-6,-7),(-2,9)
分析:将点A(-4,5)代入抛物线y=-x2+bx+5,先求出抛物线的解析式,从而求出y轴交点B的坐标,抛物线的对称轴,再根据平行线的性质求出点N的坐标.
解答:∵点A(-4,5)在抛物线y=-x2+bx+5上,
∴5=-(-4)2-4b+5,解得b=-4.
∴抛物线的解析式为y=-x2-4x+5=-(x+2)2+9,
∴抛物线的对称轴为x=-2,
∵抛物线y=-x2+bx+5与y轴交于点B,
∴点B的坐标为(0,5).
∵以A,B,M,N为顶点的四边形是平行四边形.
而点A与点B的距离是4,
∴点N的横坐标可为2或-6,或点N的纵坐标可为9,
∴点N的坐标为(2,-7)或(-6,-7)或(-2,9).
点评:本题难度较大,考查了待定系数法求抛物线的解析式,函数图象上的点的坐标与函数解析式的关系,坐标系的对称及平行四边形的性质.
分析:将点A(-4,5)代入抛物线y=-x2+bx+5,先求出抛物线的解析式,从而求出y轴交点B的坐标,抛物线的对称轴,再根据平行线的性质求出点N的坐标.
解答:∵点A(-4,5)在抛物线y=-x2+bx+5上,
∴5=-(-4)2-4b+5,解得b=-4.
∴抛物线的解析式为y=-x2-4x+5=-(x+2)2+9,
∴抛物线的对称轴为x=-2,
∵抛物线y=-x2+bx+5与y轴交于点B,
∴点B的坐标为(0,5).
∵以A,B,M,N为顶点的四边形是平行四边形.
而点A与点B的距离是4,
∴点N的横坐标可为2或-6,或点N的纵坐标可为9,
∴点N的坐标为(2,-7)或(-6,-7)或(-2,9).
点评:本题难度较大,考查了待定系数法求抛物线的解析式,函数图象上的点的坐标与函数解析式的关系,坐标系的对称及平行四边形的性质.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若反比例函数y=
(k<0)的图象经过点(-2,a),(-1,b),(3,c),则a,b,c的大小关系为( )
| k |
| x |
| A、c>a>b |
| B、b>a>c |
| C、a>b>c |
| D、c>b>a |
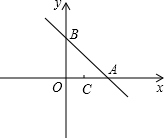 点C(1,0),且把△AOB分成两部分.
点C(1,0),且把△AOB分成两部分.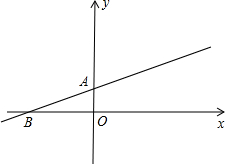 为圆心的圆与x轴相切于点C.
为圆心的圆与x轴相切于点C.