Question

如图，已知直线y=-x+2与x轴、y轴分别交于点A和点B，另已知直线y=kx+b（k≠0）经过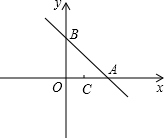点C（1，0），且把△AOB分成两部分．
（1）若△AOB被分成的两部分面积相等，求k和b的值；
（2）若△AOB被分成的两部分面积比为1：5，求k和b的值．

Answer 1

分析：（1）△AOB被分成的两部分面积相等，那么被分成的两部分都应该是三角形AOB的面积的一半，那么直线y=kx+b（k≠0）必过B点，因此根据B，C两点的函数关系式可得出，直线的函数式．
（2）若△AOB被分成的两部分面积比为1：5，那么被分成的两部分中小三角形的面积就应该是大三角形面积的

1

6

，已知了直线过C点，那么小三角形的底边是大三角形的OB边的一半，那么小三角形的高应该是OA的

1

3

，即直线经过的这点的纵坐标应该是

1

3

．那么这点应该在y轴和AB上，可分这两种情况进行计算，运用待定系数法求函数的解析式．

解答：解：（1）由题意知：直线y=kx+b（k≠0）必过C点，
∵C是OA的中点，
∴直线y=kx+b一定经过点B，C，把B，C的坐标代入可得：

b=2 k+b=0

，
解得k=-2，b=2；

（2）∵S_△AOB=

1

2

×2×2=2，
∵△AOB被分成的两部分面积比为1：5，那么直线y=kx+b（k≠0）与y轴或AB交点的纵坐标就应该是：2×2×

1

6

=

2

3

，
当y=kx+b（k≠0）与直线y=-x+2相交时：
当y=

2

3

时，直线y=-x+2与y=kx+b（k≠0）的交点的横坐标就应该是-x+2=

2

3

，
∴x=

4

3

，
即交点的坐标为（

4

3

，

2

3

），
又根据C点的坐标为（1，0），可得：

4 3 k+b= 2 3 k+b=0

，
∴

k=2 b=-2

，
当y=kx+b（k≠0）与y轴相交时，交点的坐标就应该是（0，

2

3

），又有C点的坐标（1，0），可得：

k+b=0 b= 2 3

，
∴

k=- 2 3 b= 2 3

，
因此：k=2，b=-2或k=-

2

3

，b=

2

3

．

点评：本题的关键是弄清楚三角形AOB被分成两部分的面积比不同时，所求直线与y轴和已知直线的交点的纵坐标是多少．