题目内容
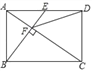
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() .
.
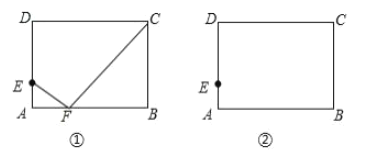
(1)当![]() 时,
时,![]() 上存在点
上存在点![]() ,使
,使![]() 与
与![]() 相似,求
相似,求![]() 的长度.
的长度.
(2)对于每一个确定的![]() 的值
的值![]() 上存在几个点
上存在几个点![]() 使得
使得![]() 与
与![]() 相似?
相似?
【答案】(1)![]() 或3;(2)当
或3;(2)当![]() 且
且![]() 时,有3个;当
时,有3个;当![]() 时,有2个;当
时,有2个;当![]() 时,有2个;当
时,有2个;当![]() 时,有1个.
时,有1个.
【解析】
(1)分△AEF∽△BFC和△AEF∽△BCF两种情形,分别构建方程即可解决问题;
(2)根据题意画出图形,交点个数分类讨论即可解决问题;
解:(1)当∠AEF=∠BFC时,
要使△AEF∽△BFC,需![]() ,即
,即![]() ,
,
解得AF=1或3;
当∠AEF=∠BCF时,
要使△AEF∽△BCF,需![]() ,即
,即![]() ,
,
解得AF=1;
综上所述AF=1或3.
(2)如图,延长DA,作点E关于AB的对称点E′,连结CE′,交AB于点F1;
连结CE,以CE为直径作圆交AB于点F2、F3.
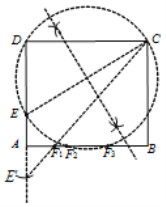
当m=4时,由已知条件可得DE=3,则CE=5,
即图中圆的直径为5,
可得此时图中所作圆的圆心到AB的距离为2.5,等于所作圆的半径,F2和F3重合,
即当m=4时,符合条件的F有2个,
当m>4时,图中所作圆和AB相离,此时F2和F3不存在,即此时符合条件的F只有1个,
当1<m<4且m≠3时,由所作图形可知,符合条件的F有3个,
综上所述:
当1<m<4且m≠3时,有3个;
当m=3时,有2个;
当m=4时,有2个;
当m>4时,有1个.

练习册系列答案
相关题目