题目内容
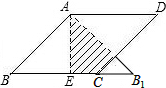 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是考点:菱形的性质,翻折变换(折叠问题)
专题:
分析:首先设CD与AB1交于点O,由在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,可求得AE的长,继而求得△ABB1、△AEB1、△COB1的面积.则可求得答案.
解答: 解:如图,设CD与AB1交于点O,
解:如图,设CD与AB1交于点O,
∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=
,
由折叠易得△ABB1为等腰直角三角形,
∴S△ABB1=
BA•AB1=2,S△ABE=1,
∴CB1=2BE-BC=2
-2,
∵AB∥CD,
∴∠OCB1=∠B=45°,
又由折叠的性质知,∠B1=∠B=45°,
∴CO=OB1=2-
.
∴S△COB1=
OC•OB1=3-2
,
∴重叠部分的面积为:2-1-(3-2
)=2
-2.
 解:如图,设CD与AB1交于点O,
解:如图,设CD与AB1交于点O,∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=
| 2 |
由折叠易得△ABB1为等腰直角三角形,
∴S△ABB1=
| 1 |
| 2 |
∴CB1=2BE-BC=2
| 2 |
∵AB∥CD,
∴∠OCB1=∠B=45°,
又由折叠的性质知,∠B1=∠B=45°,
∴CO=OB1=2-
| 2 |
∴S△COB1=
| 1 |
| 2 |
| 2 |
∴重叠部分的面积为:2-1-(3-2
| 2 |
| 2 |
点评:此题考查了菱形的性质以及等腰直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
郑州地铁,是郑州市第一个轨道运输系统.根据规划,由六条线路组成,预计总投资1000亿元.1000亿元用科学记数法表示为(保留两个有效数字)( )
| A、1×1010元 |
| B、1×1011元 |
| C、1.0×1010元 |
| D、1.0×1011元 |
在实数1.414,π,2+
,
,-
,0.101001000…中,无理数有( )
| 3 |
| 3 | 9 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |