Question

反比例函数y=

k

x

的图象在第一象限的分支上有一点A（2，3），P为x轴正半轴上的一个动点．
（1）求反比例函数的解析式；
（2）当P在什么位置时，△OPA直角三角形，求出此时P点的坐标．

Answer 1

分析：（1）将A（2，3）代入y=

k

x

可得k的值，进而可得函数解析式；
（2）可分两种情况：①当∠OHA=90°时，易得；②当∠OAP=90°时，过A作AH⊥x轴于H，易得△OAH∽△APH，进而可得

OH

AH

=

AH

PH

；化简代入数据可得答案．

解答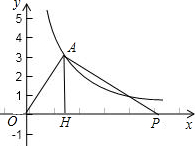：解：（1）将A（2，3）代入y=

k

x

，（1分）
得K=6，所以函数解析式为y=

6

x

；（2分）

（2）当∠OHA=90°时，H（2，0）；
当∠OAP=90°时，过A作AH⊥x轴于H，
由△OAH∽△APH，（4分）
得

OH

AH

=

AH

PH

；
即PH=

AH2

OH

=

32

2

=

9

2

；
所以，OP=2+

9

2

=

13

2

；
此时，点P的坐标为（

13

2

，0）．（5分）

点评：此题综合考查了反比例函数，正比例函数等多个知识点．此题难度稍大，综合性比较强，注意对各个知识点的灵活应用．