题目内容
已知二次函数 (a、m为常数,且a¹0)。
(a、m为常数,且a¹0)。
(1)求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;
(2)设该函数的图像的顶点为C,与x轴交于A、B两点,与y轴交于点D。
①当△ABC的面积等于1时,求a的值:
②当△ABC的面积与△ABD的面积相等时,求m的值。
 (a、m为常数,且a¹0)。
(a、m为常数,且a¹0)。(1)求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;
(2)设该函数的图像的顶点为C,与x轴交于A、B两点,与y轴交于点D。
①当△ABC的面积等于1时,求a的值:
②当△ABC的面积与△ABD的面积相等时,求m的值。
(1)见解析(2)①a=-8或a=8② 或
或 或
或
 或
或 或
或
解:(1)证明: ,
,
令 ,即
,即
∵当a¹0时, 。
。
∴方程 有两个不相等的实数根。
有两个不相等的实数根。
∴当a¹0时,不论a与m为何值,该函数的图像与x轴总有两个公共点。
(2)①∵ ,
,
∴点C的坐标为( ,
, )。
)。
当y=0时, 。解得x1=m,x2=m+1。所以AB=1。
。解得x1=m,x2=m+1。所以AB=1。
△ABC的面积等于1时, 。
。
∴ ,或
,或 。
。
∴a=-8或a=8。
②当x=0时,y= am2+am,所以点D的坐标为(0, am2+am)。
当△ABC的面积与△ABD的面积相等时, 。
。
∴ 或
或 。
。
∴ 或
或 或
或 。
。
(1)由一元二次方程根的判别式大于0进行证明。
(2)①根据△ABC的面积等于1列方程 求解。
求解。
②根据△ABC的面积与△ABD的面积相等列方程 求解。
求解。
 ,
,令
 ,即
,即
∵当a¹0时,
 。
。∴方程
 有两个不相等的实数根。
有两个不相等的实数根。∴当a¹0时,不论a与m为何值,该函数的图像与x轴总有两个公共点。
(2)①∵
 ,
,∴点C的坐标为(
 ,
, )。
)。当y=0时,
 。解得x1=m,x2=m+1。所以AB=1。
。解得x1=m,x2=m+1。所以AB=1。△ABC的面积等于1时,
 。
。∴
 ,或
,或 。
。∴a=-8或a=8。
②当x=0时,y= am2+am,所以点D的坐标为(0, am2+am)。
当△ABC的面积与△ABD的面积相等时,
 。
。∴
 或
或 。
。∴
 或
或 或
或 。
。(1)由一元二次方程根的判别式大于0进行证明。
(2)①根据△ABC的面积等于1列方程
 求解。
求解。②根据△ABC的面积与△ABD的面积相等列方程
 求解。
求解。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点(2,2)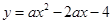 交x轴的正半轴于点A,交y轴于点B,且OA=OB.
交x轴的正半轴于点A,交y轴于点B,且OA=OB.
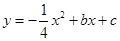 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结
,连结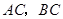 ,
, 是线段
是线段 上一动点,以
上一动点,以 为一边向右侧作正方形
为一边向右侧作正方形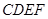 ,连结
,连结 .若
.若 ,
, .
.
 ;
; 的度数;
的度数; 时,点
时,点 也随着运动,则点
也随着运动,则点 的图象与
的图象与 轴交于B、C两点(点B在点C的左侧),一次函数
轴交于B、C两点(点B在点C的左侧),一次函数 的图象经过点B和二次函数图象上另一点A. 点A的坐标(4 ,3),
的图象经过点B和二次函数图象上另一点A. 点A的坐标(4 ,3),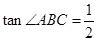 .
.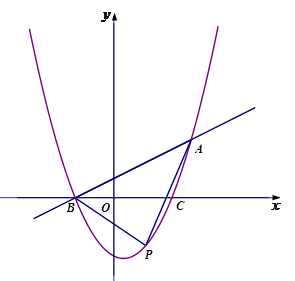
 面积S的最大值并求出此时点P的坐标;
面积S的最大值并求出此时点P的坐标;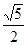 倍,求点M的坐标.
倍,求点M的坐标. (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是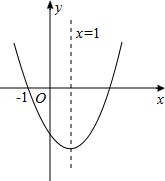
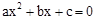 (a≠0)的一个根
(a≠0)的一个根
 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;