Question

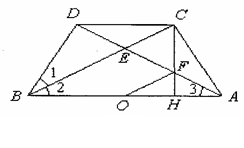
如图所示，已知AD与BC相交于E，∠1=∠2=∠3，BD=CD，∠ADB=90°，CH⊥AB于H，CH交AD于F．

(1)求证：CD∥AB；

(2)求证：△BDE≌△ACE；

(3)若O为AB中点，求证：OF=BE．

 

Answer 1

证明：(1)∵BD=CD，∴∠BCD=∠1．∵ ∠l=∠2，∠BCD=∠2．∴CD∥AB．

    (2) ∵ CD∥AB  ∴∠CDA=∠3．

      ∠BCD=∠2=∠3．且BE=AE．且∠CDA=∠BCD．∴DE=CE．

      在△BDE和△ACE中， DE=CE，∠DEB=∠CEA，BE=AE．∴△BDE≌△ACE

    (3) ∵△BDE≌△ACE

       ∠4=∠1，∠ACE=∠BDE=90°．

∴∠ACH=90°一∠BCH

       又CH⊥AB，．∴ ∠2=90°一∠BCH

∴∠ACH=∠2=∠1=∠4．AF=CF

∵∠AEC=90°一∠4，∠ECF=90°一∠ACH

      ∠ACH=∠4 ∠AEC=∠ECF．CF=EF．∴ EF=AF

       O为AB中点，OF为△ABE的中位线    ∴OF=BE