题目内容
15.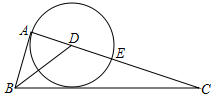 如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E
如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E(1)求证:BC是⊙D的切线;
(2)若AB=5,BC=13,求CE的长.
分析 (1)过点D作DF⊥BC于点F,根据角平分线的性质得到AD=DF.根据切线的判定定理即可得到结论;
(2)根据切线的性质得到AB=FB.根据和勾股定理列方程即可得到结论.
解答 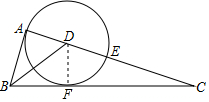 (1)证明:过点D作DF⊥BC于点F,
(1)证明:过点D作DF⊥BC于点F,
∵∠BAD=90°,BD平分∠ABC,
∴AD=DF.
∵AD是⊙D的半径,DF⊥BC,
∴BC是⊙D的切线;
(2)解:∵∠BAC=90°.
∴AB与⊙D相切,
∵BC是⊙D的切线,
∴AB=FB.
∵AB=5,BC=13,
∴CF=8,AC=12.
在Rt△DFC中,
设DF=DE=r,则
r2+64=(12-r)2,
解得:r=$\frac{10}{3}$.
∴CE=$\frac{16}{3}$.
点评 本题考查了切线的判定,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5. 如图所示,直线y=kx+b(k≠0)与x轴交于点(-5,0),则关于x的方程kx+b=0的解为x=( )
如图所示,直线y=kx+b(k≠0)与x轴交于点(-5,0),则关于x的方程kx+b=0的解为x=( )
 如图所示,直线y=kx+b(k≠0)与x轴交于点(-5,0),则关于x的方程kx+b=0的解为x=( )
如图所示,直线y=kx+b(k≠0)与x轴交于点(-5,0),则关于x的方程kx+b=0的解为x=( )| A. | -5 | B. | -4 | C. | 0 | D. | 1 |
6.已知OA是表示北偏东50°方向的一条射线,则OA的反向延长线表示的是( )
| A. | 北偏西50°方向上的一条射线 | B. | 北偏西40°方向上的一条射线 | ||
| C. | 南偏西40°方向上的一条射线 | D. | 南偏西50°方向上的一条射线 |
10.反比例函数y=-$\frac{3}{x}$的图象上有P1(x1,-2),P2(x2,-3)两点,则x1与x2的大小关系是( )
| A. | x1<x2 | B. | x1=x2 | C. | x1>x2 | D. | 不确定 |
20.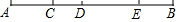 如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )
如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )
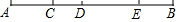 如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )
如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( )| A. | CD=3 | B. | DE=2 | C. | CE=5 | D. | EB=5 |
