题目内容
 如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB=
如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB=考点:全等三角形的性质
专题:
分析:由△ACB的内角和定理求得∠CAB=25°;然后由全等三角形的对应角相等得到∠EAD=∠CAB=25°.则结合已知条件易求∠EAB的度数;最后利用△AEB的内角和是180度和图形来求∠DEF的度数.
解答:解:如图,∵∠ACB=105°,∠B=50°,
∴∠CAB=180°-∠B-∠ACB=180°-50°-105°=25°.
又∵△ABC≌△ADE,
∴∠EAD=∠CAB=25°.
又∵∠EAB=∠EAC+∠CAD+∠CAB,∠CAD=10°,
∴∠EAB=25°+10°+25°=60°,即∠EAB=60°.
∴∠AEB=180°-∠EAB-∠B=180°-60°-50°=70°,
∴∠EDF=∠AED-∠AEB=105°-70°=35°.
故答案是:60;35.
∴∠CAB=180°-∠B-∠ACB=180°-50°-105°=25°.
又∵△ABC≌△ADE,
∴∠EAD=∠CAB=25°.
又∵∠EAB=∠EAC+∠CAD+∠CAB,∠CAD=10°,
∴∠EAB=25°+10°+25°=60°,即∠EAB=60°.
∴∠AEB=180°-∠EAB-∠B=180°-60°-50°=70°,
∴∠EDF=∠AED-∠AEB=105°-70°=35°.
故答案是:60;35.
点评:本题考查全等三角形的性质.全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.

练习册系列答案
相关题目
 如图,在?ABCD中,E,F为AC上两点,BE∥DF.求证:四边形BEDF为平行四边形.
如图,在?ABCD中,E,F为AC上两点,BE∥DF.求证:四边形BEDF为平行四边形. 在如图边长为7.6的正方形的角上挖掉一个边长为2.6的小正方形.
在如图边长为7.6的正方形的角上挖掉一个边长为2.6的小正方形.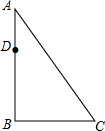 如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是30m,求树高AB.
如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是30m,求树高AB.